The Fourier transform is a fundamental tool for understanding signal and image content, modeling, and filter design. On this page, you will find some simple examples illustrating simple relations between signal and images and their corresponding Fourier transform. The examples are made in Matlab R2021b. The Fourier spectrum is the function of lengths of the complex elements in the Fourier transform. In Matlab, this is calculated using the abs function. Also, in all examples, the fftshift function has been used to reorder the output of the fft function, such that the origin is in the center of the signal or image.
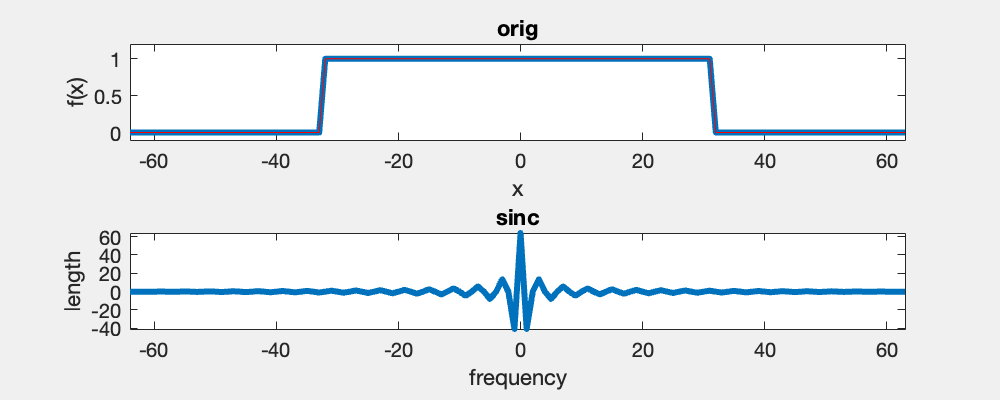
Here you see an example of a 1D box function and its Fourier transform. Since the box is an even function, then its Fourier transform is real.
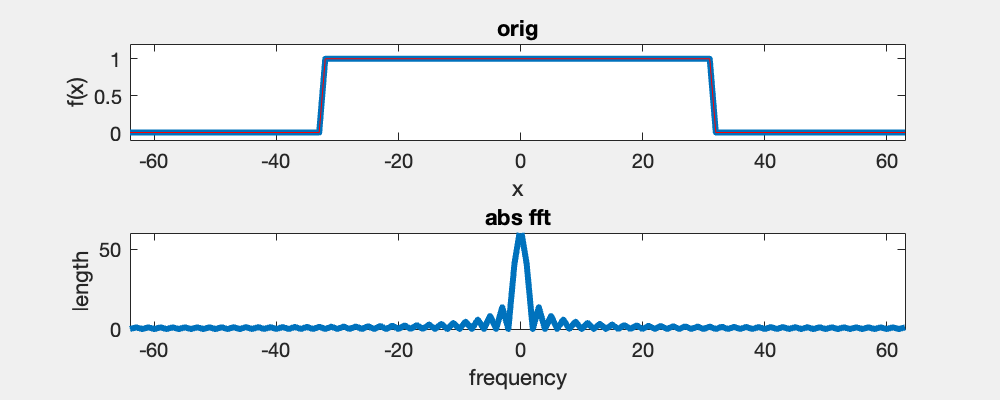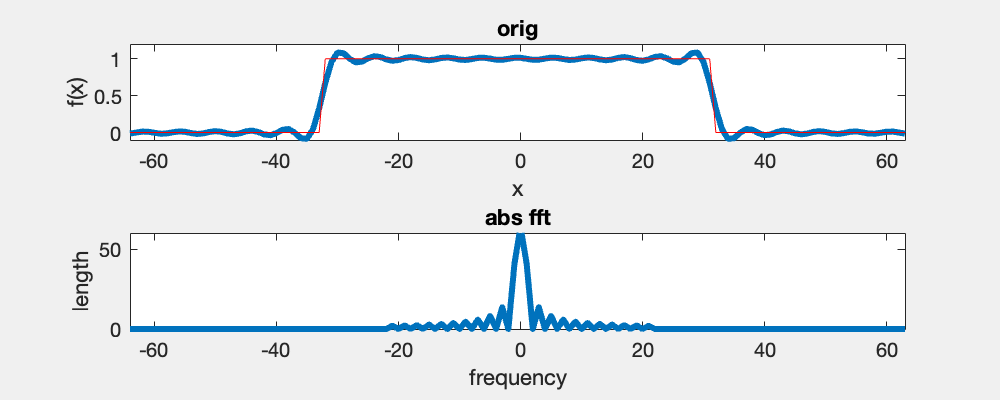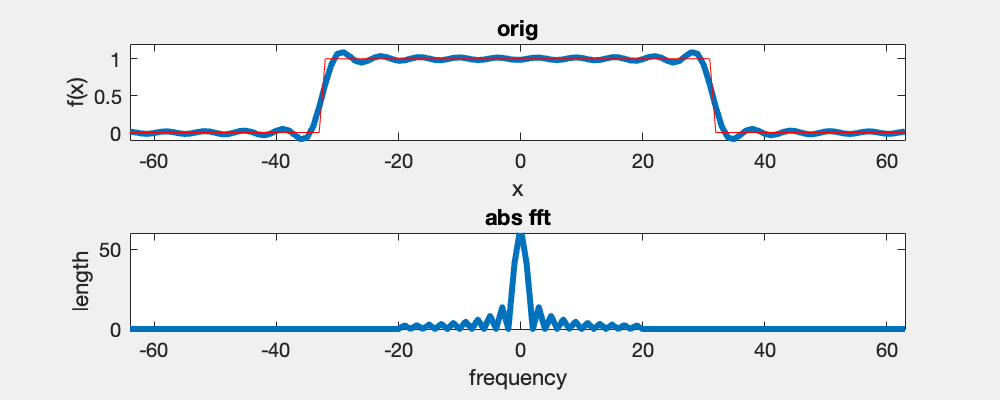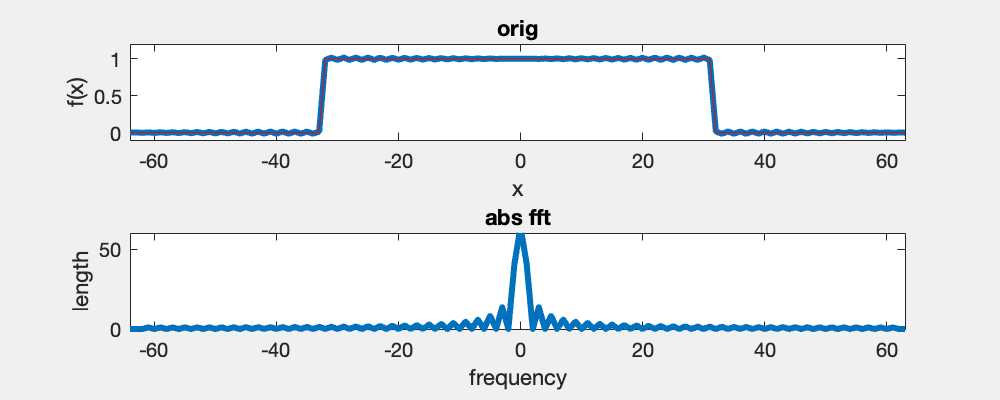
Here you see an example of a 1D box function and its Fourier spectrum using the fft and fftshift functions in Matlab. In the video, I iteratively remove high-frequency components symmetrically from the left and right.
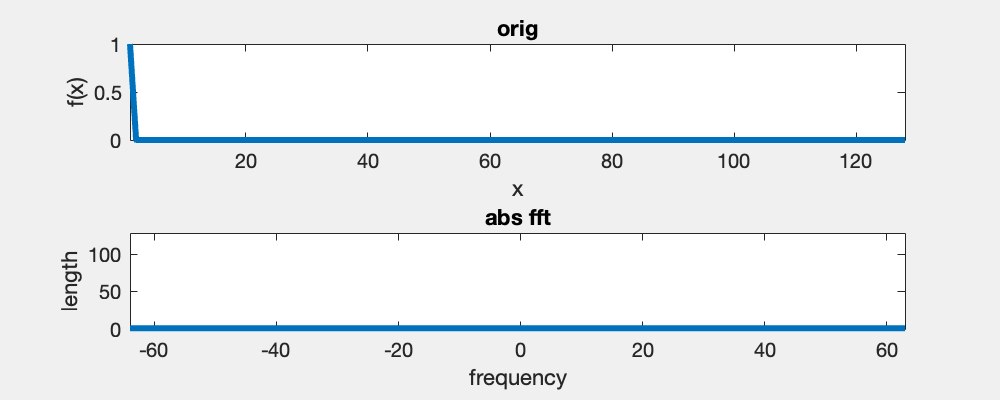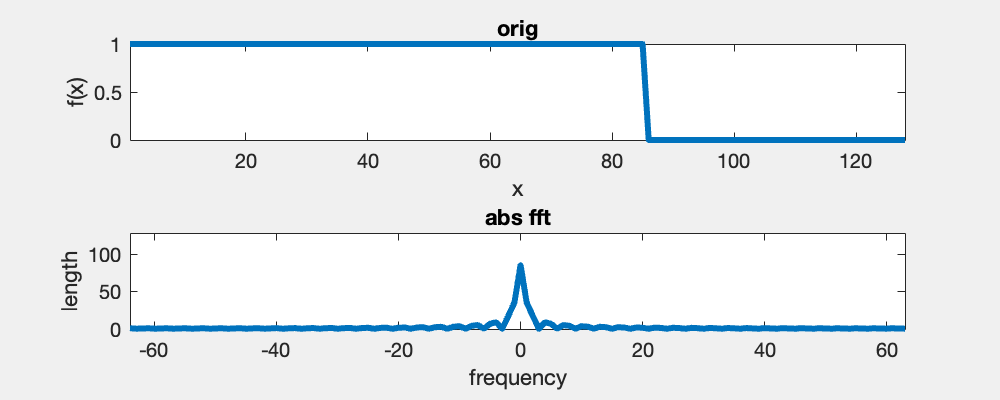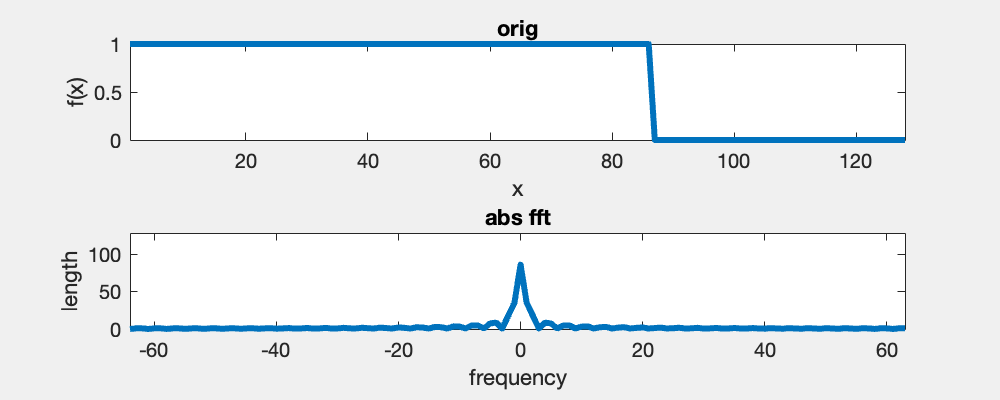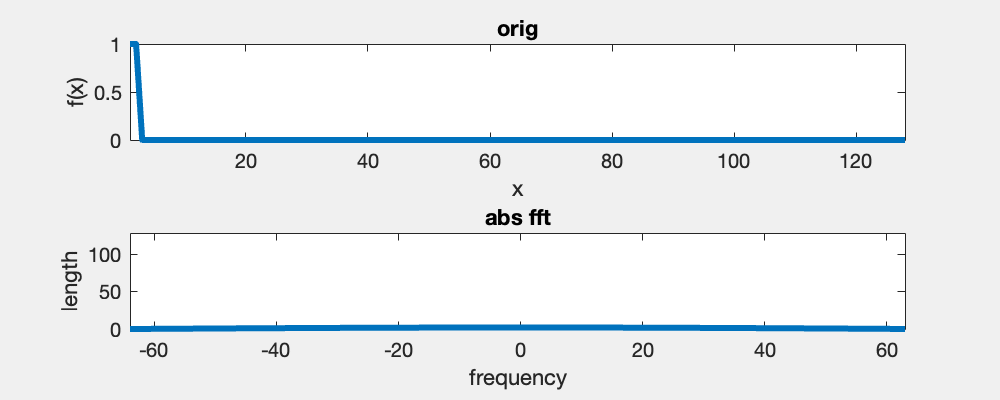
The Fourier transform of a box function is a sinc function (sinc(x)=sin(x)/x), and the wavelength is proportional to the width of the box function. The Fourier transform assumes the signal to be periodic and a horizontal translation of the box does not change its Fourier spectrum.
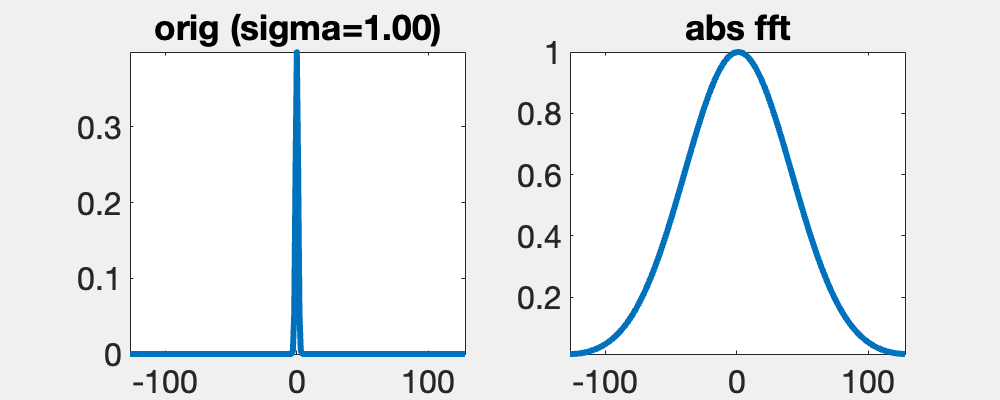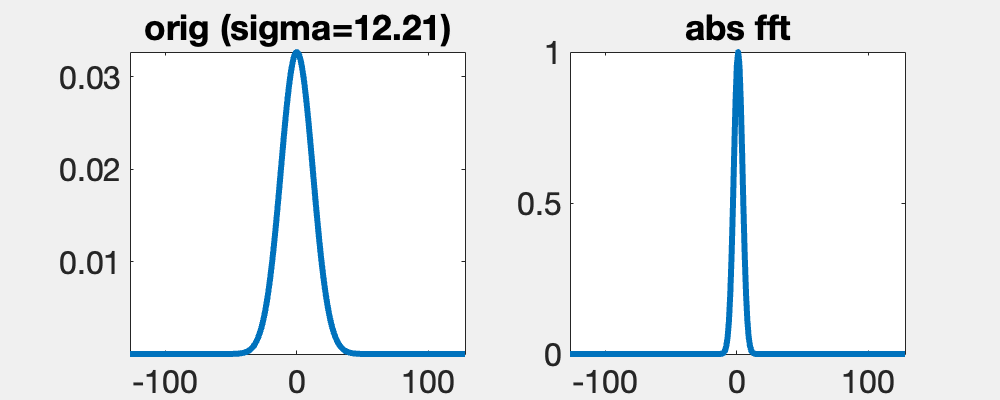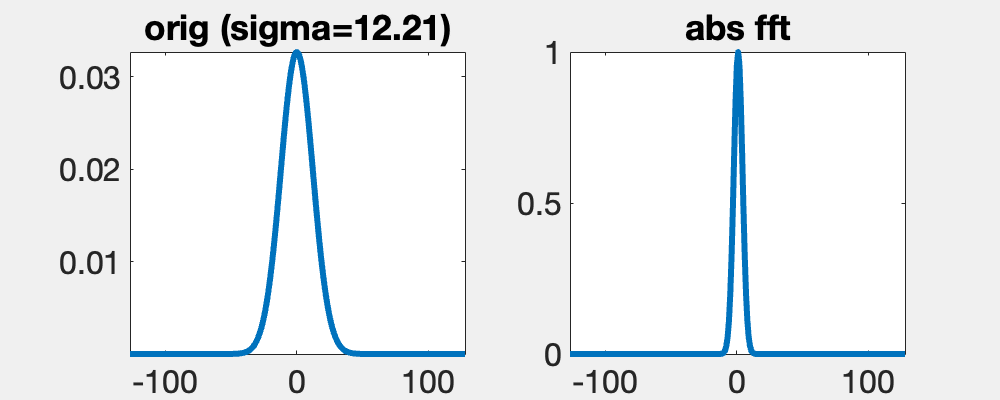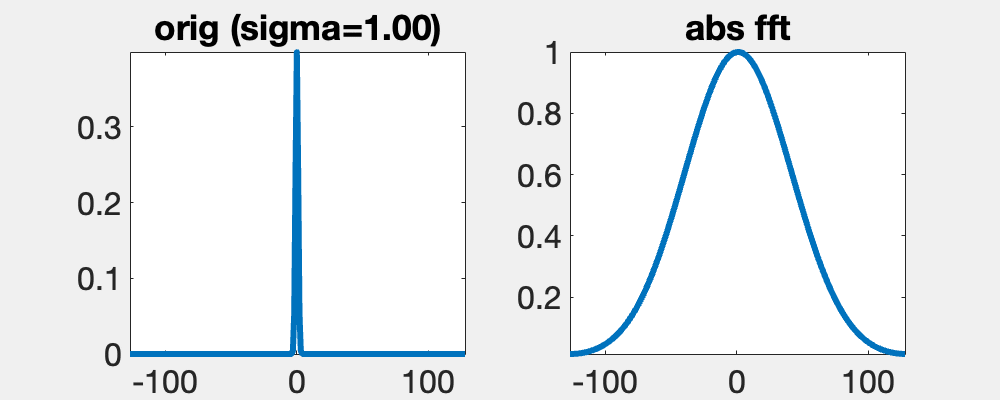
The Gauss function f(x) = exp(-x^2/(2 s^2))/sqrt(2 pi s^2), here of width s, is unqiue, since its Fourier transform, F, is also a Gauss function. The transformed has a width 1/s. Since F(0) = int f(x) dx, if the integral of f is constant then integral of F is not.

A consequence of Fourier series is that images are modeled as being periodic. Hence, the right-most pixel's right neighbor is its left-most, and the top-most top neighbor is the bottom-most. Note that this animation correctly illustrates the topological relations of a flat image living on a torus, but the local distances are warped on the torus as compared to the flat image.
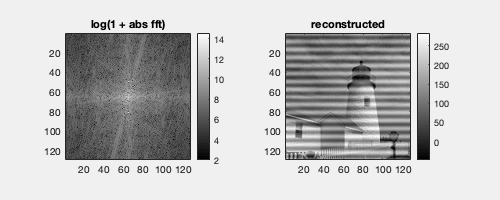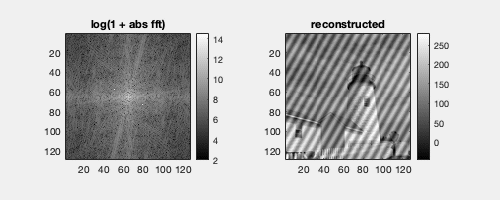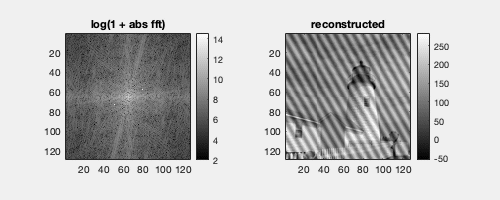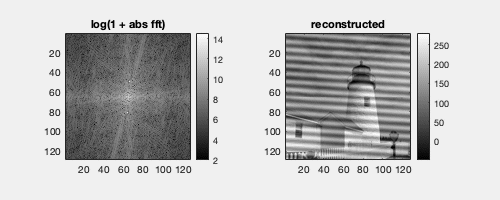
An image with an added cosine wave will have 2 symmetrical peaks in the Fourier domain. Their location corresponds to the direction of the corresponding wave in the image, and the distance from the center in the Fourier domain corresponds inversely to the wavelength in the spatial domain.
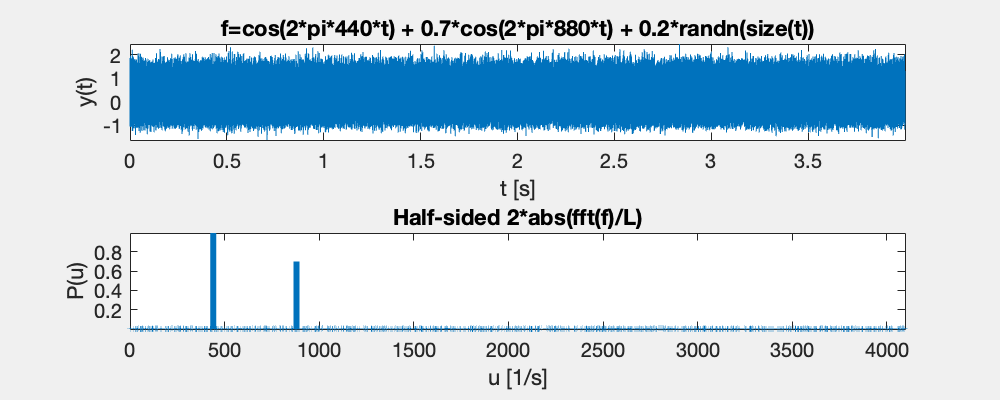
The coefficients of the original cosine functions can be retrieved by simple calculations with the power spectrum.
Differentiation in the spatial domain to any order is in practice filtering. Simple manipulations of the invers Fourier transform will reveal that the n'th order derivative in the spatial domain is the same as multiplication of a n'th degree monomial in the frequency domain.
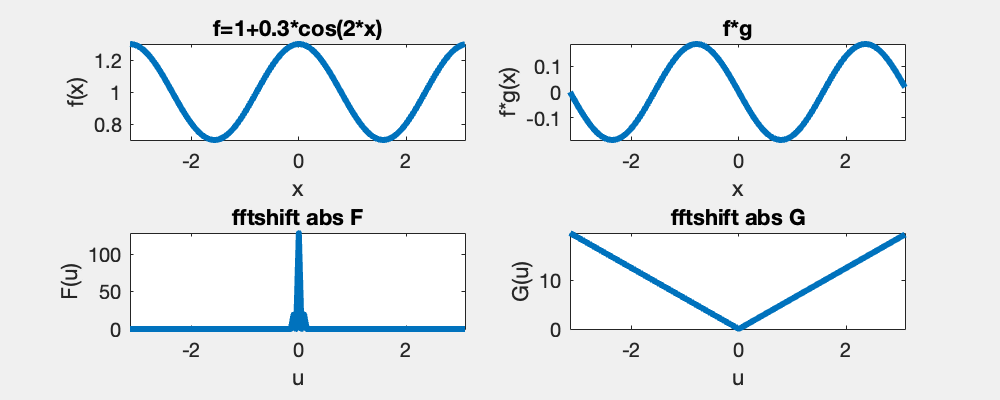
A consequence of the convolution theorem, Fourier(f*g) = Fourier(f)Fourier(g). And since the Fourier transform of a Gaussian is another Gaussian with the inverse width, smoothing with a Gaussian of width s in the spatial domain is the same as multiplying in the Fourier domain with a Gaussian of width 1/s. Hence, as seen here, a little smoothing removes a few frequencies, but a lot removes a many.
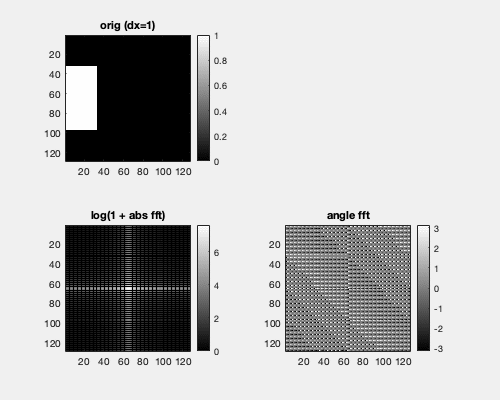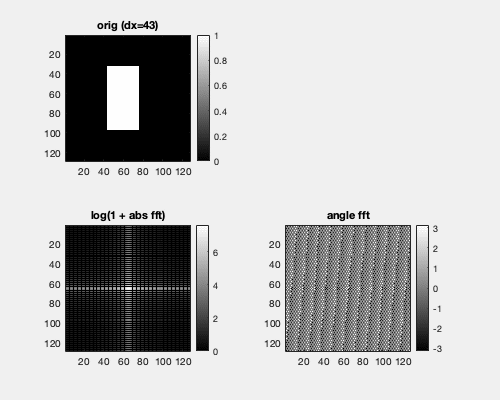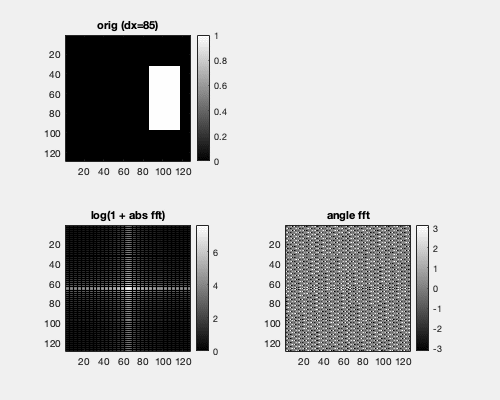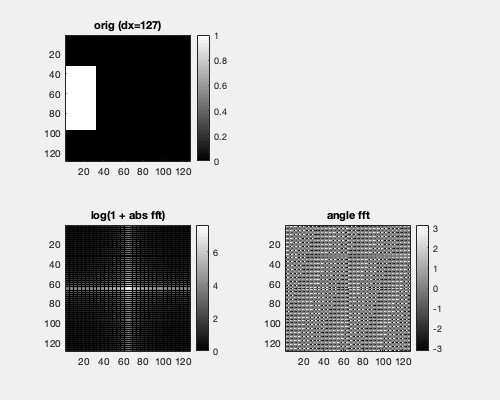
Fourier transformation considers signals as periodic. A consequence is that the neighbor of the rightmost pixel is the leftmost pixel at the same height. Hence, here we translate a box horizontally, and we see that the Fourier spectrum is not changed.
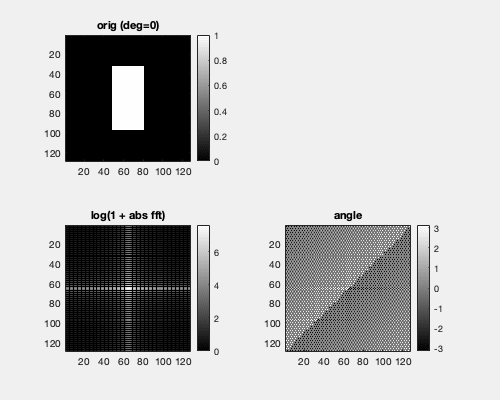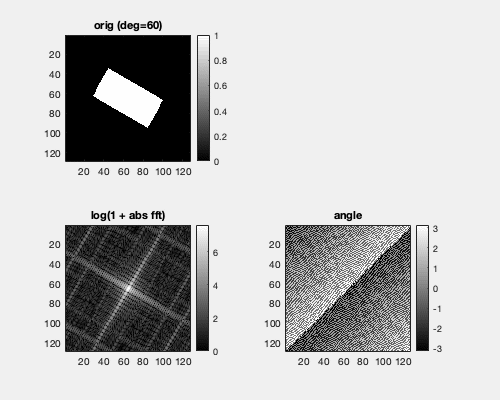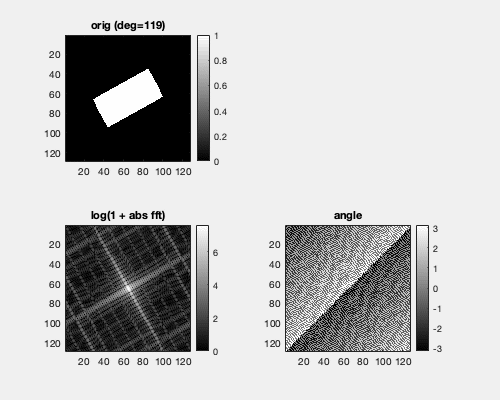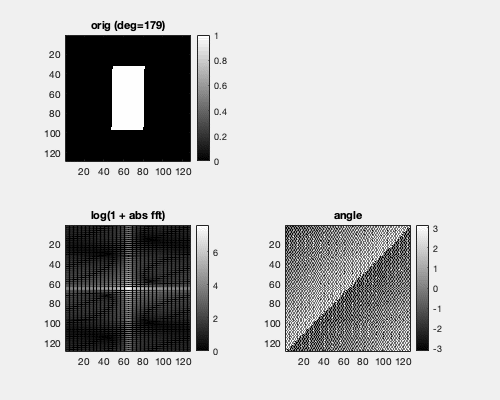
Each point in the Fourier domain corresponds to a planar wave in the spatial domain. Hence, rotating a box in the spatial domain gives a similar rotation in the Fourier domain.

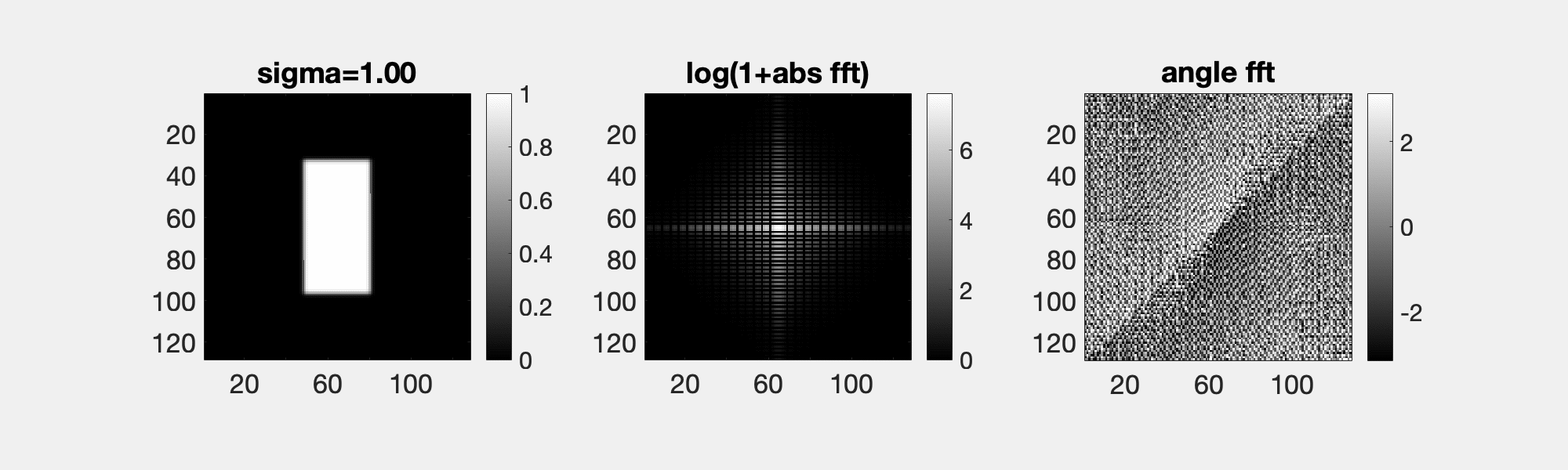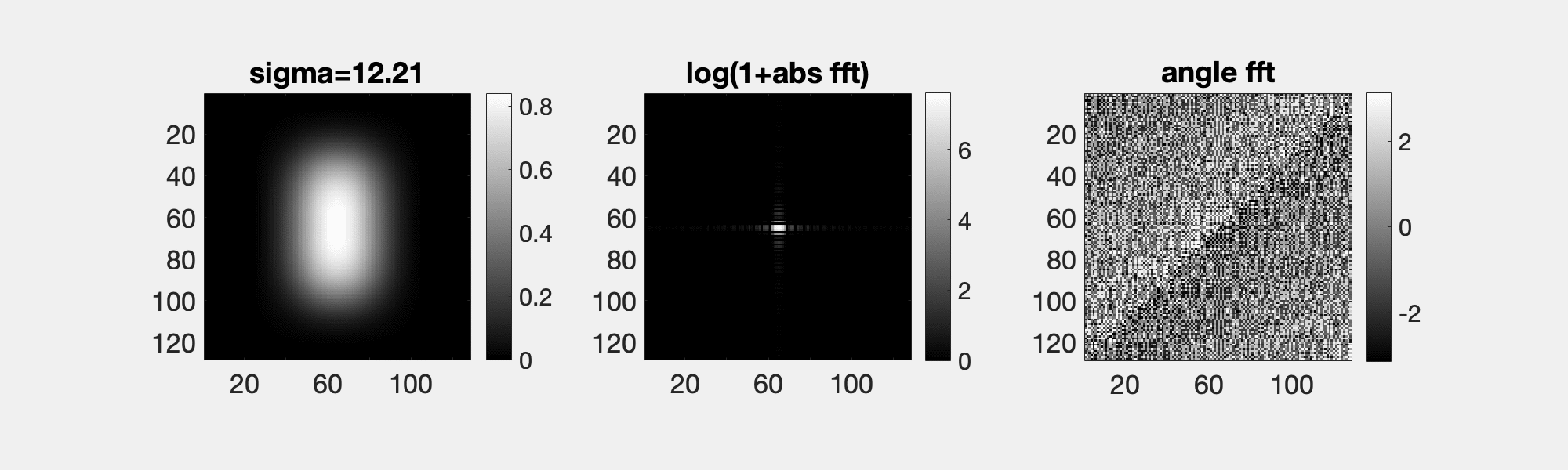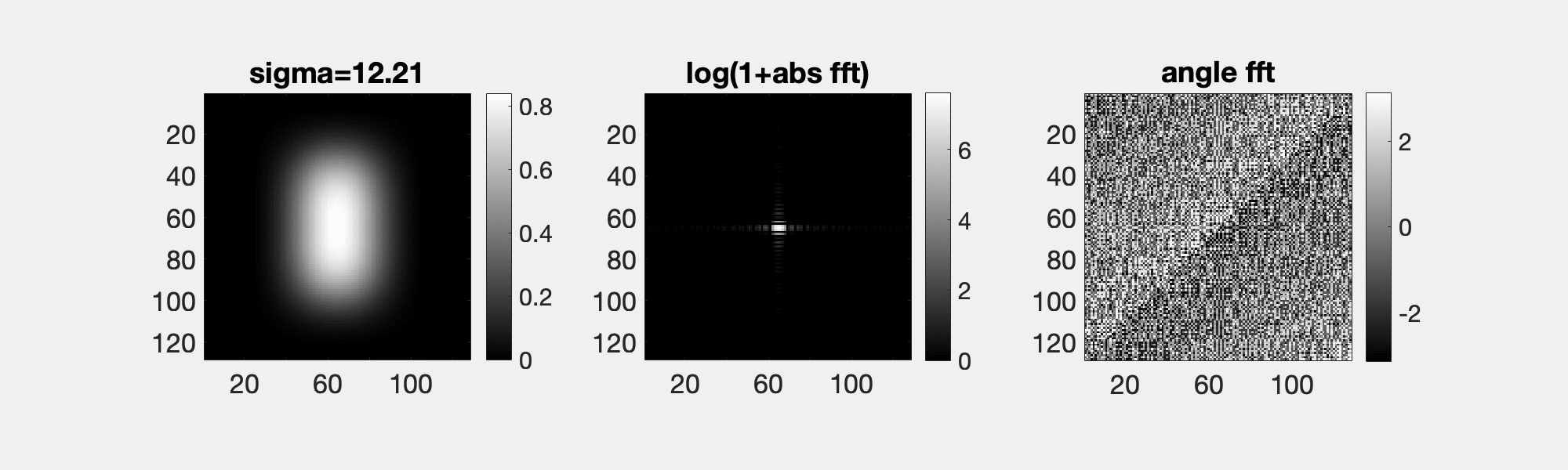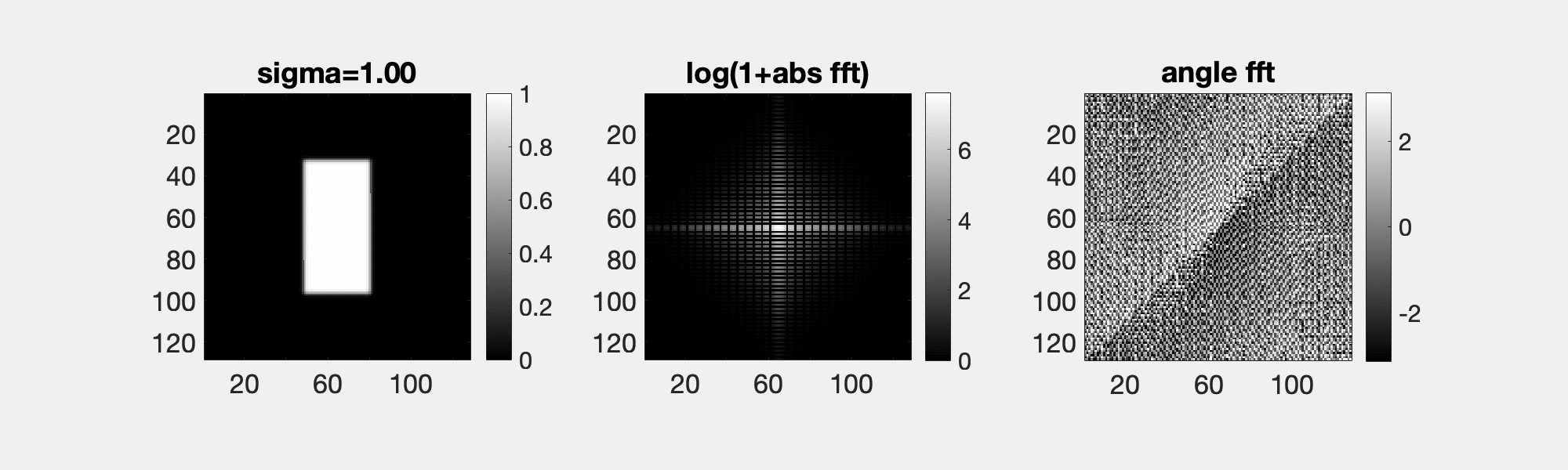
This is not an animated gif. Replacing the length of a Fourier transform of an image with a generic exp(-r) function does not completely destroy the image. However, replacing the angle component with independently and identically distributed noise does.
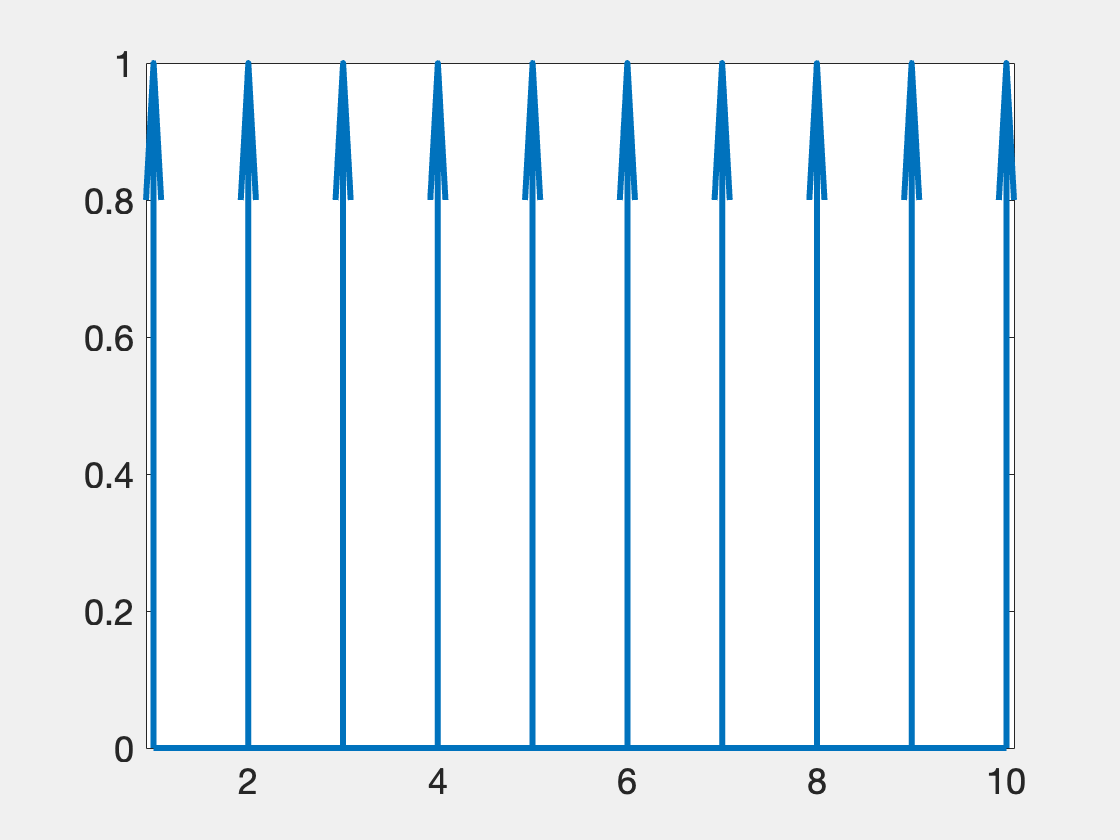
The Dirac comb is an infinit series of Dirac's delta functions, which are evenly spaced appart with a distance T. It is an even function and it's Fourier transform is also a Dirac comb (not shown here), and it's spacing is 1/T.
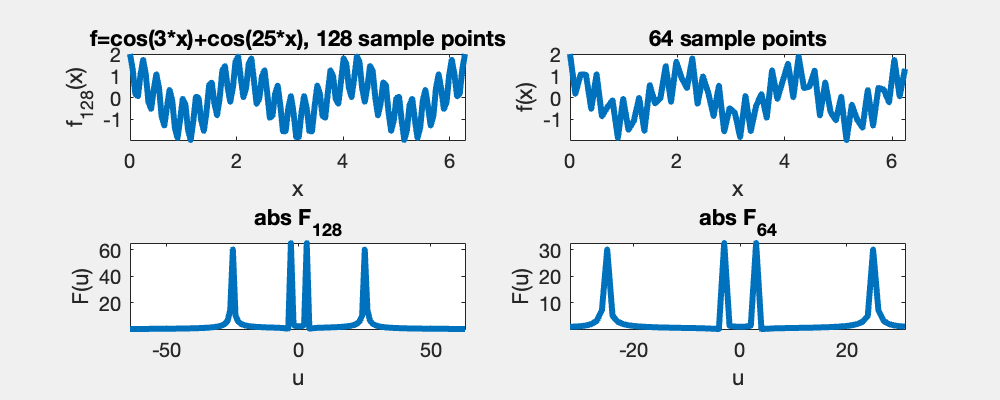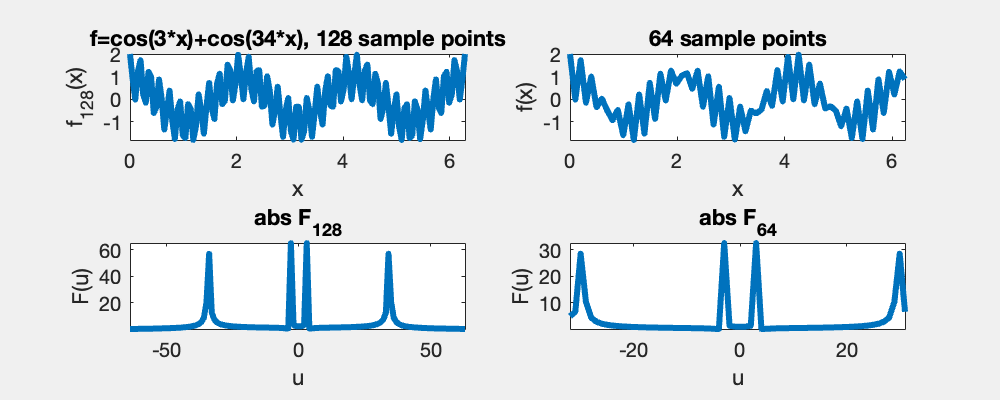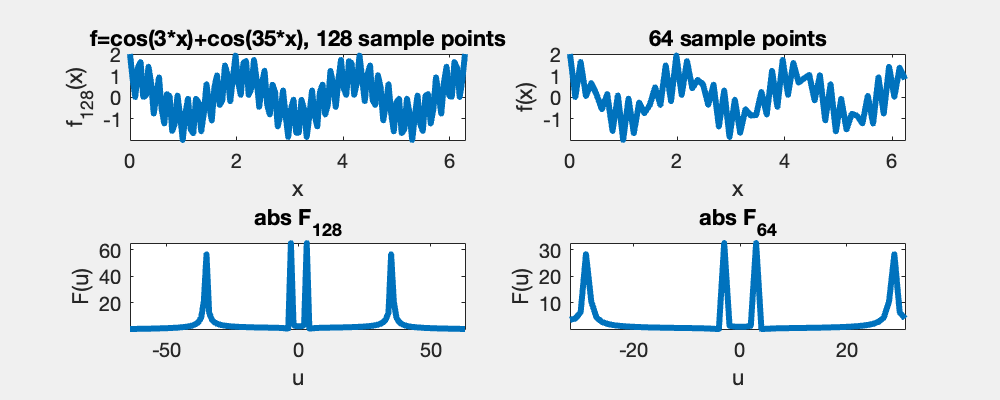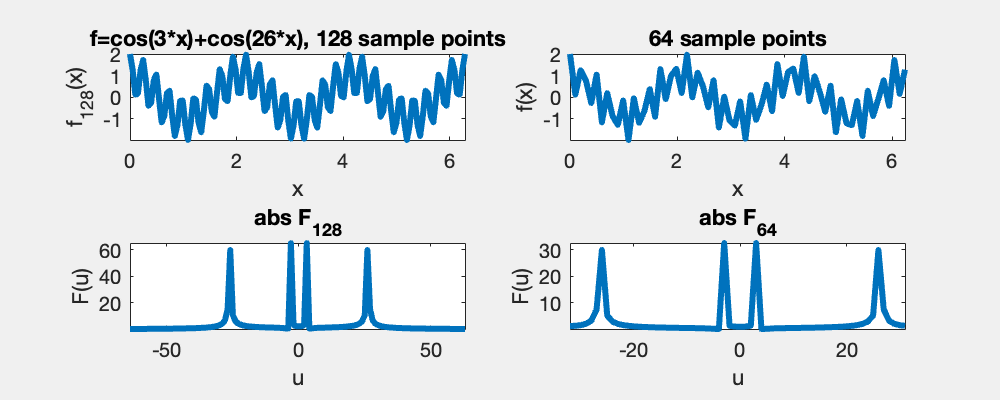
A consequence of Nyquist's theorem is that for signals sampled with a sampling frequency below the Nyquist's critical frequency, the higher frequencies are wrapped and falsely identified as lower frequency. In this demo, the left column shows the correct frequencies in the power specturm while the right shows that the high frequencies bouncing back, when they cross Nyquist's critical frequency.
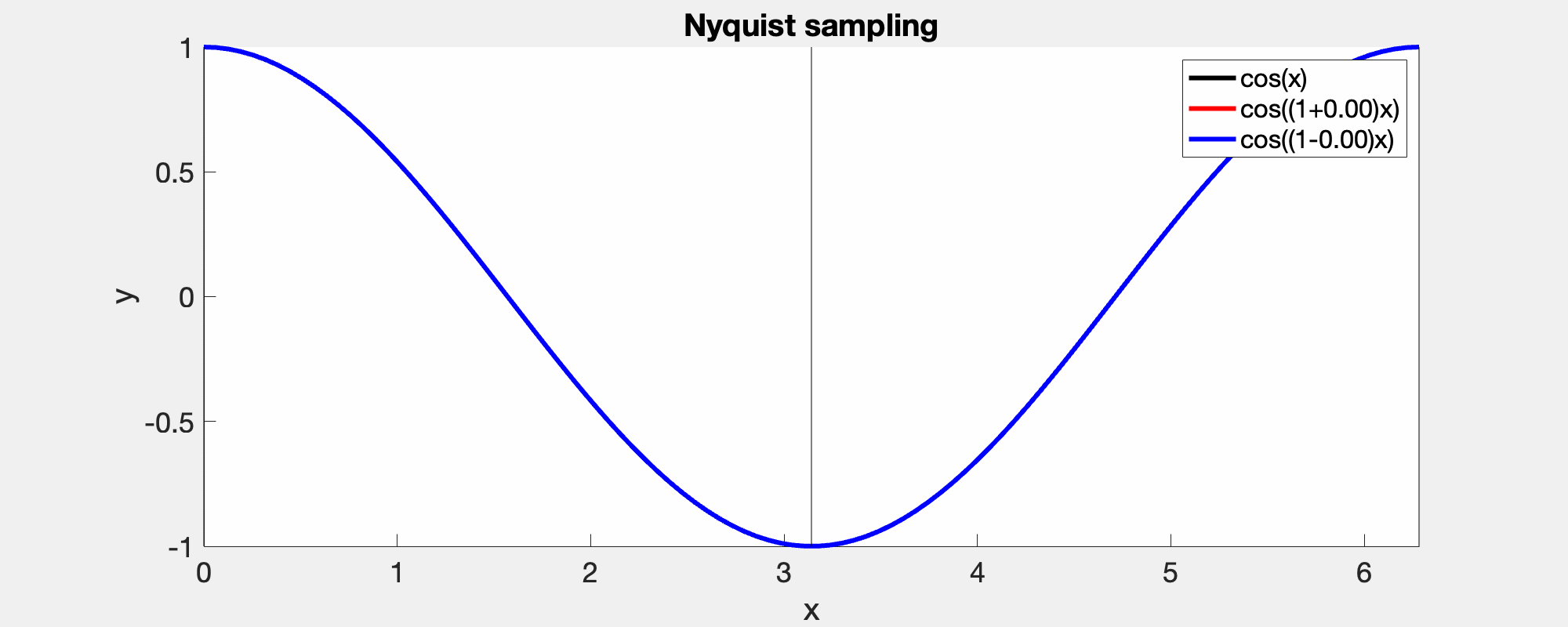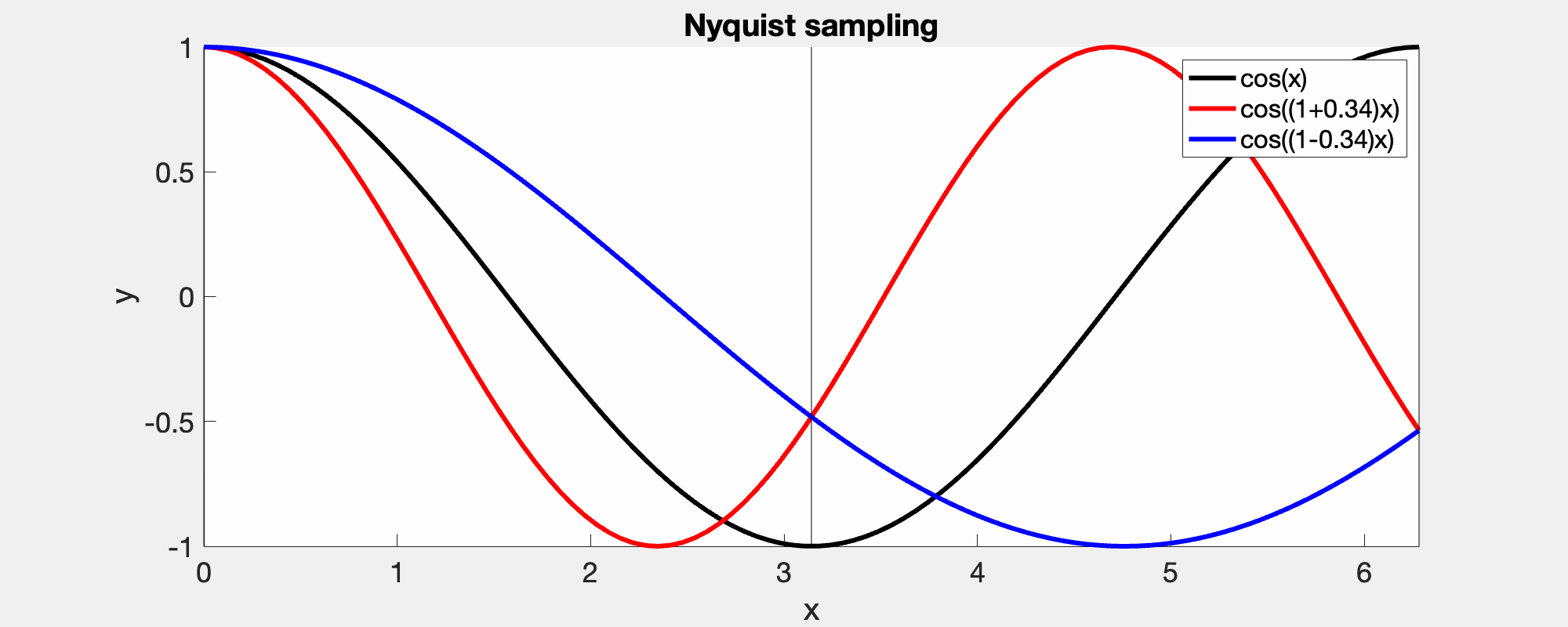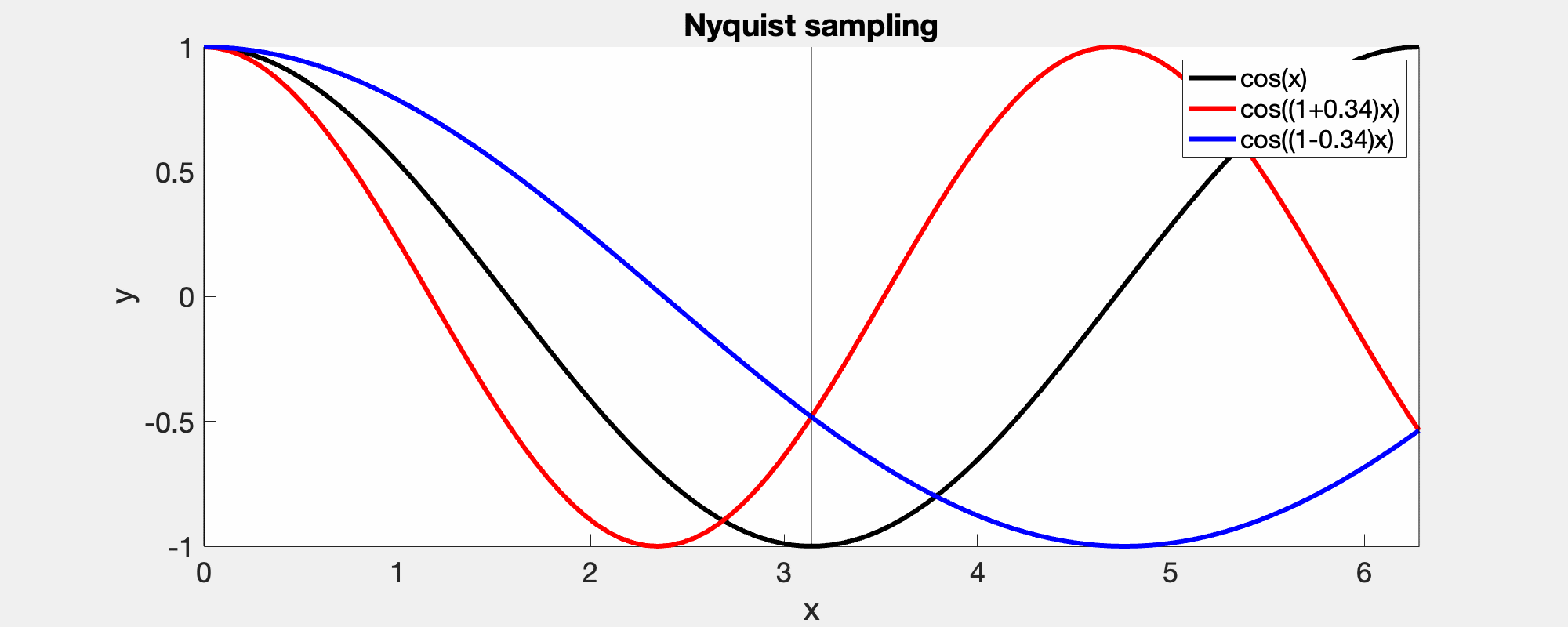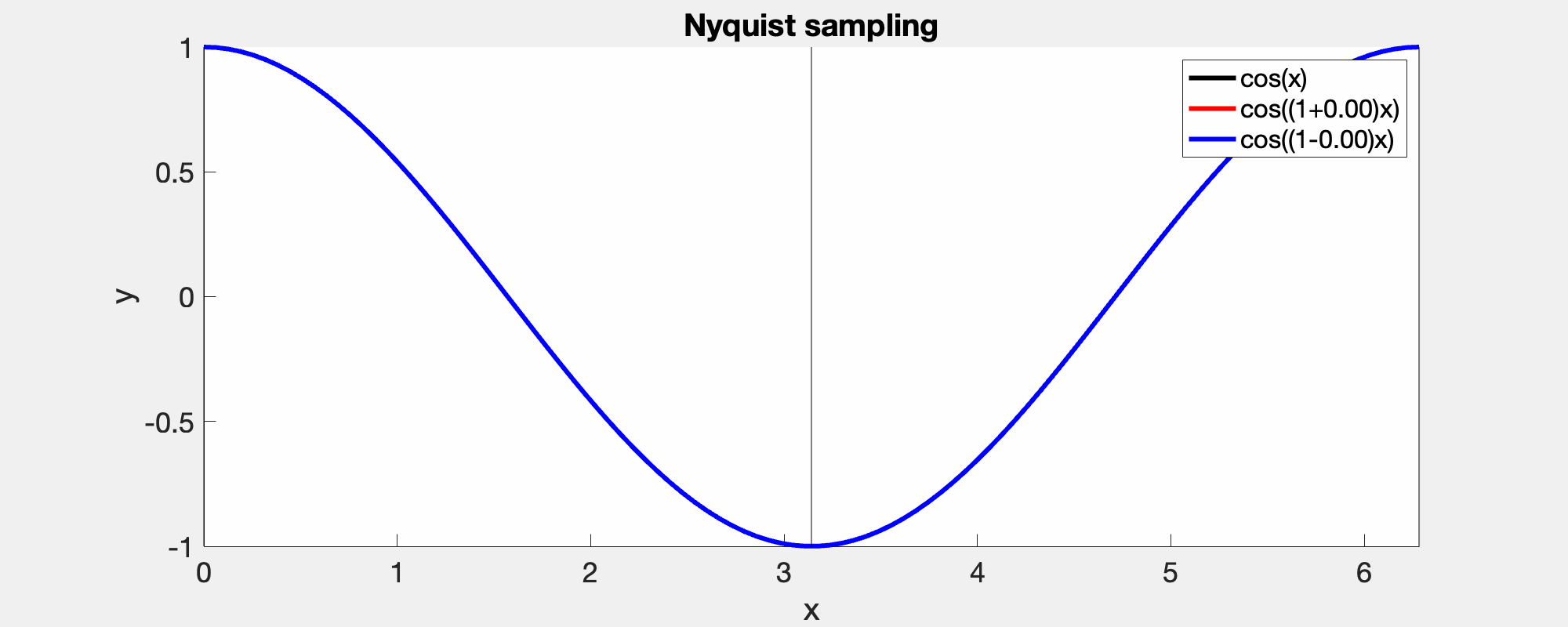
A given sampling frequency can only identify waves below the Nyquist frequency. Those above, cannot be distinguished from those below, i.e., the red and the blue curve meet at the sample points [0, pi, 2pi].
Mathematical morphology for binary images is a tool for working with neighbourhoods of white and black pixels. It is often used in conjunction with binary segmentation, where each pixel has been classified according to whether it belongs to a segment or not.
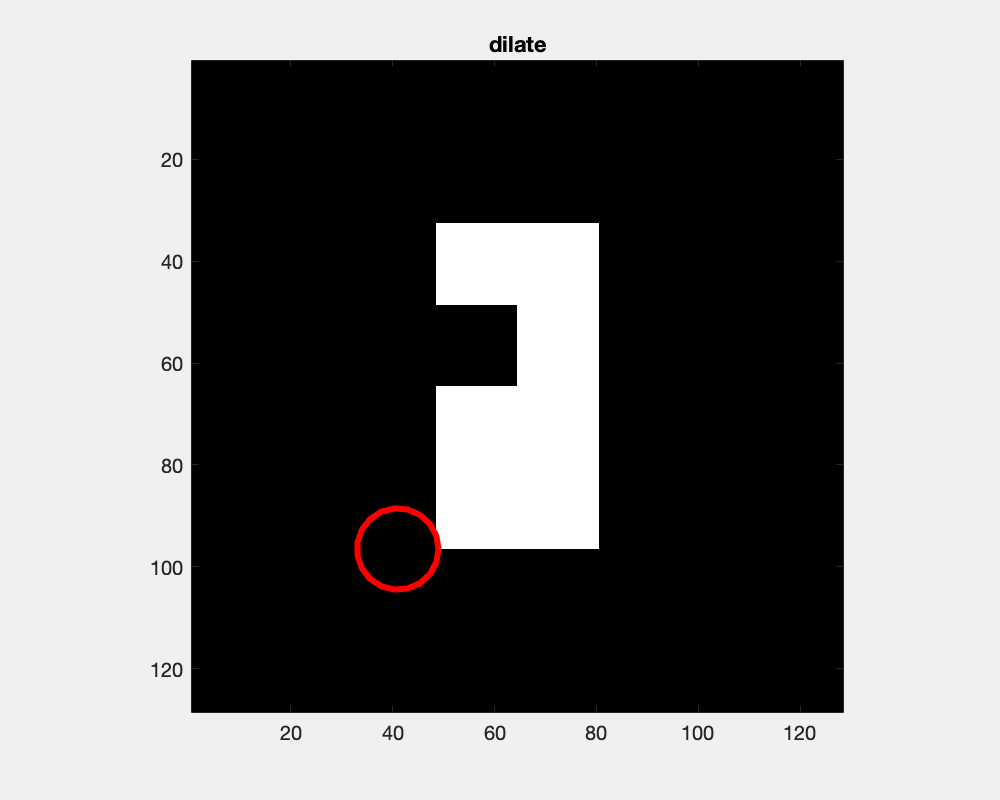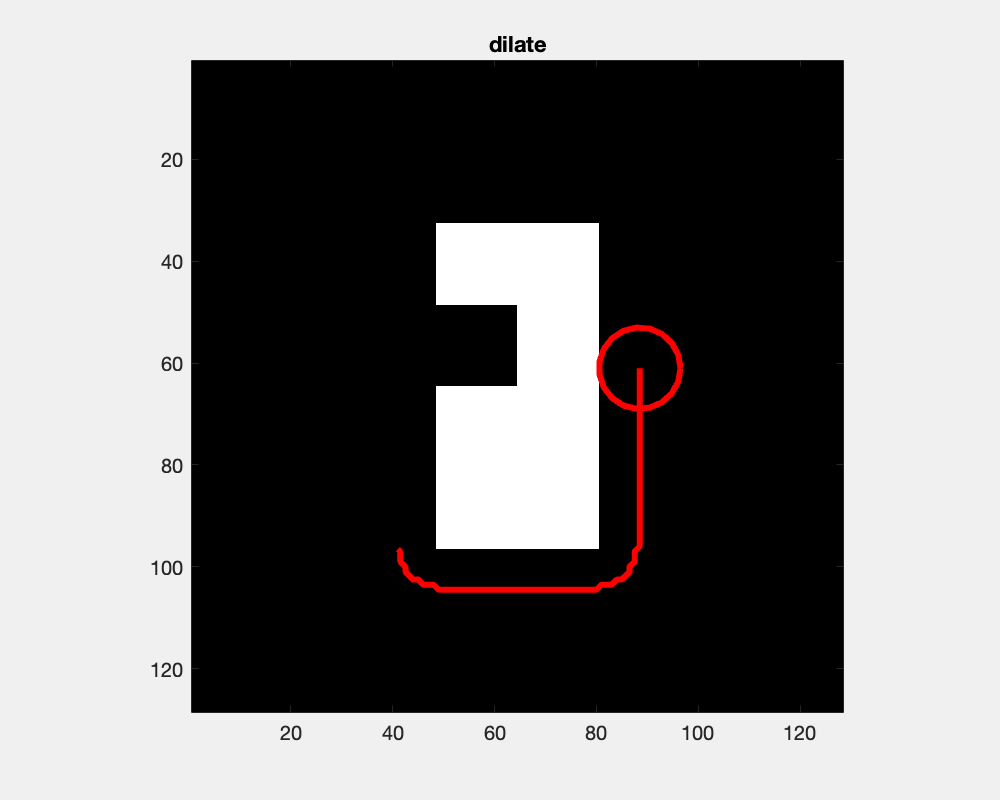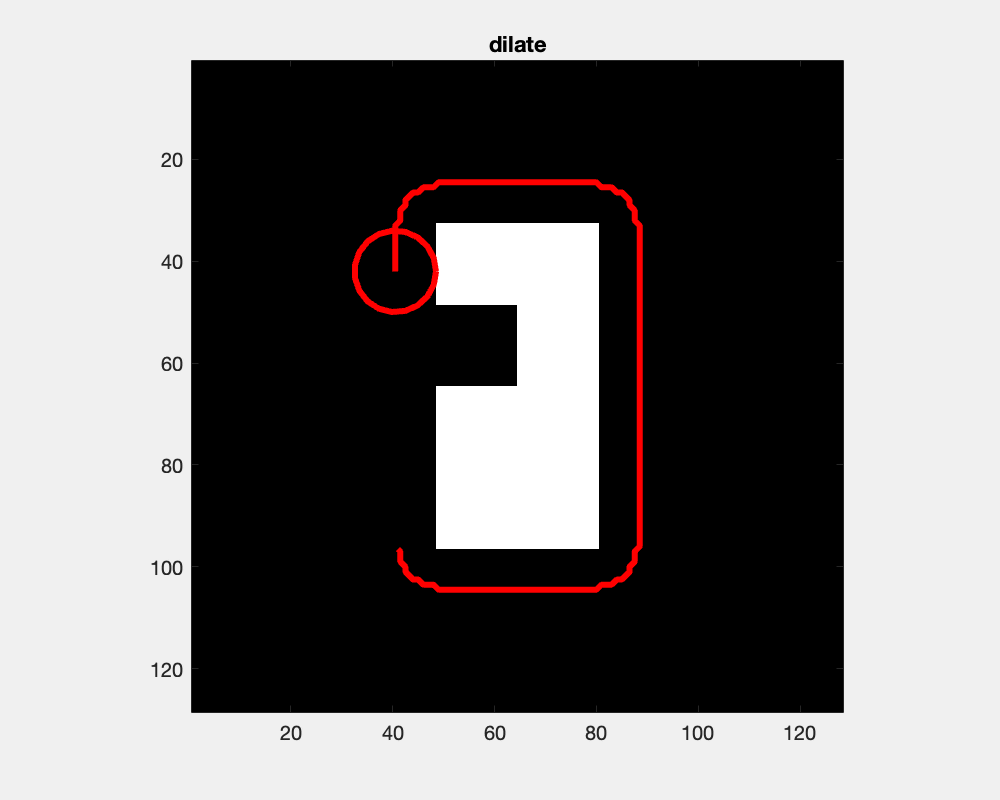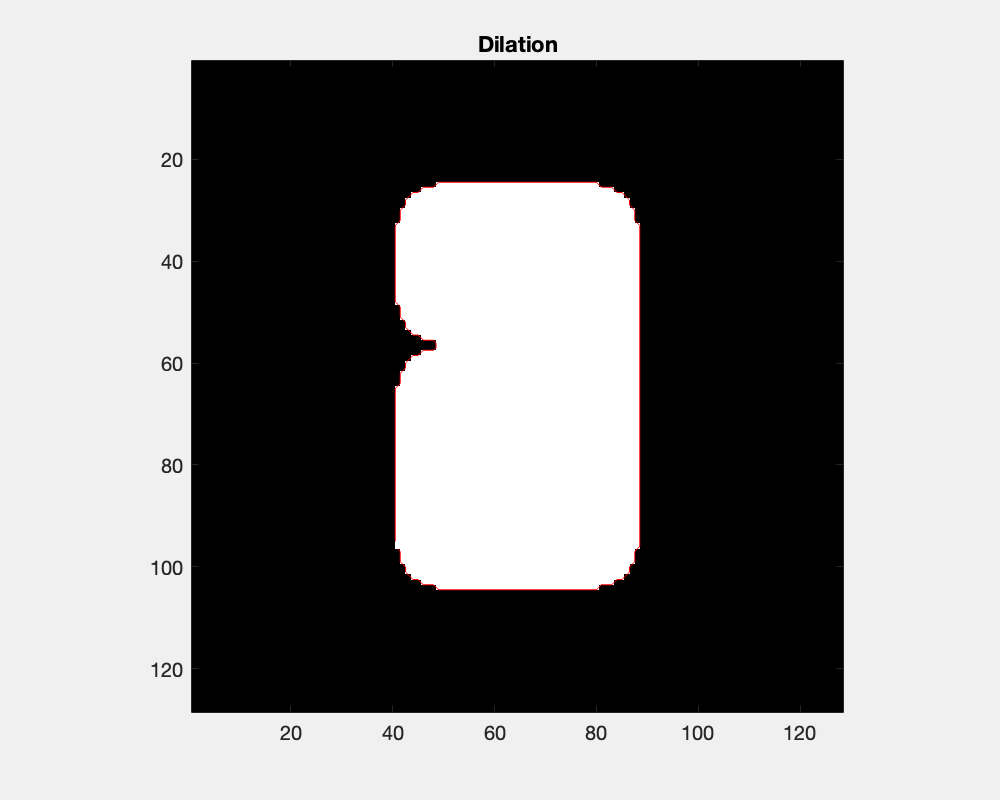
The effect of dilation with a disc-shaped structuring element can be envisioned as the locus of anchor points, here the center of the disc, as the element skims the surface on the outside of an object.
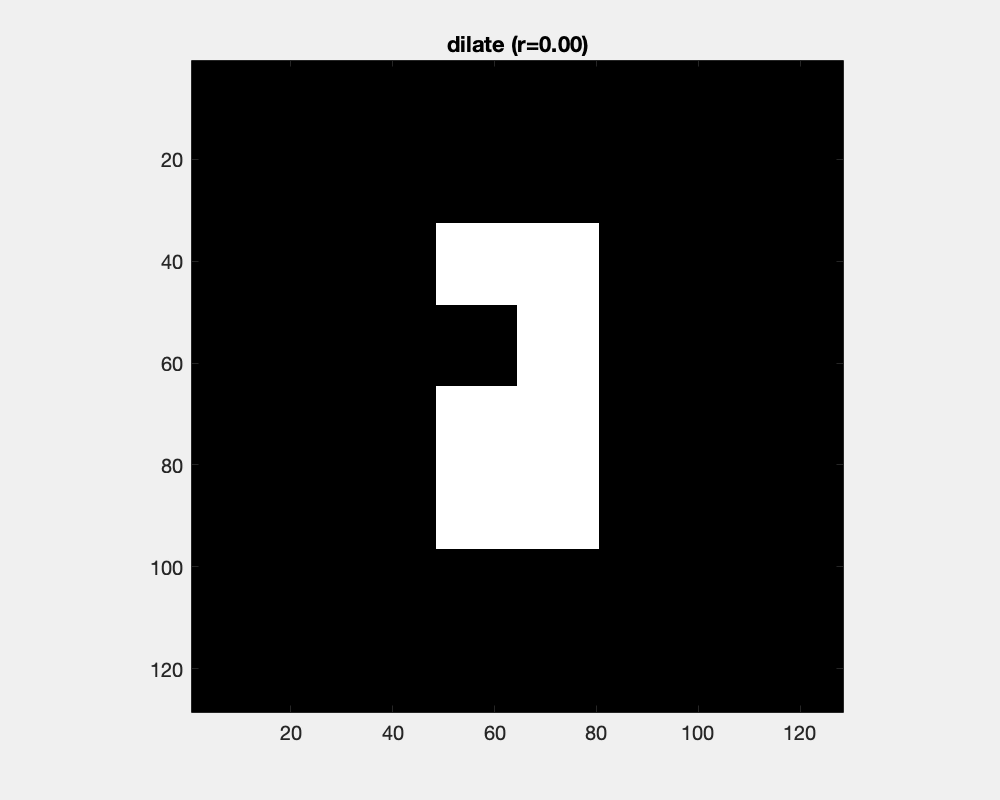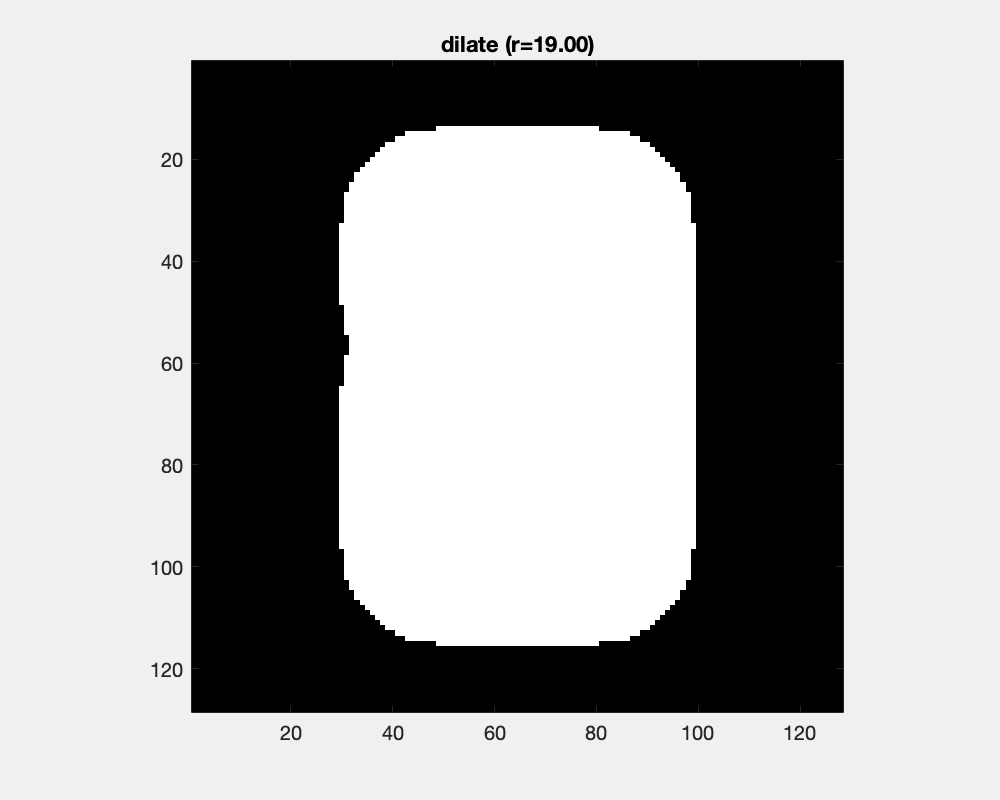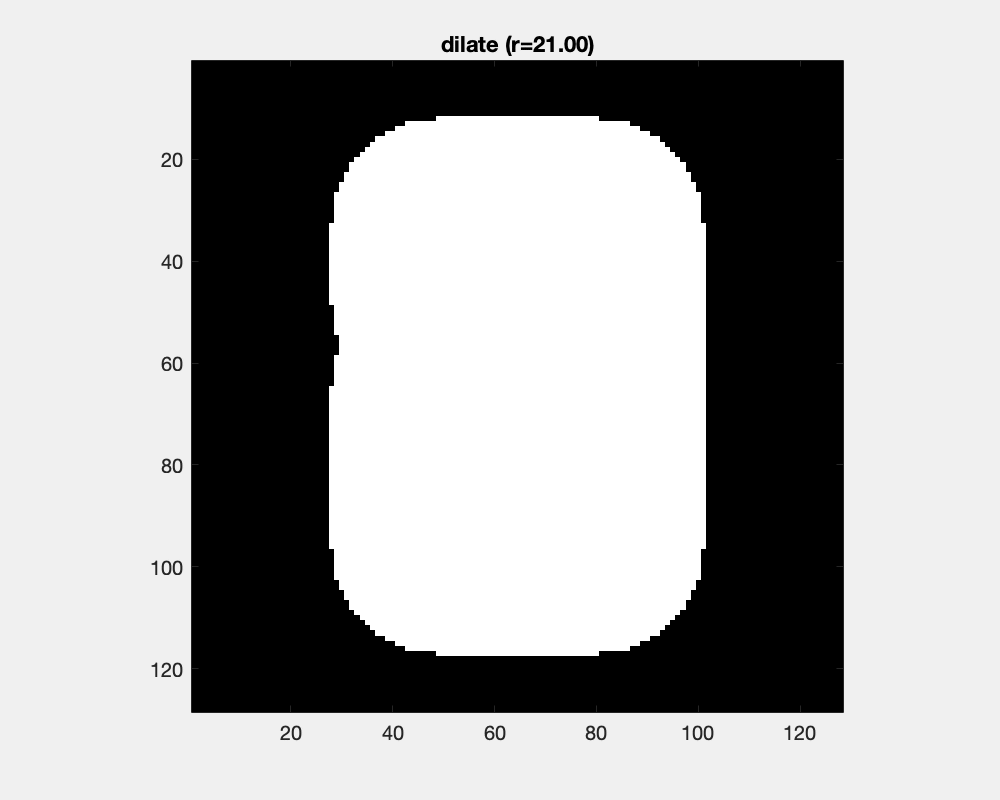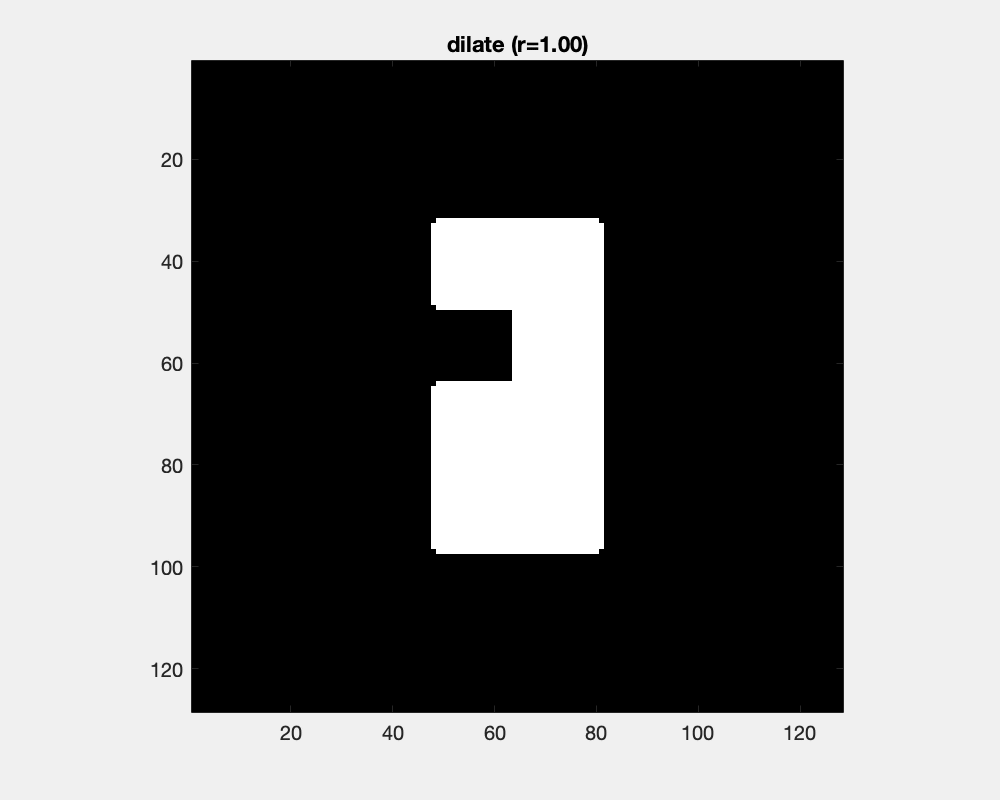
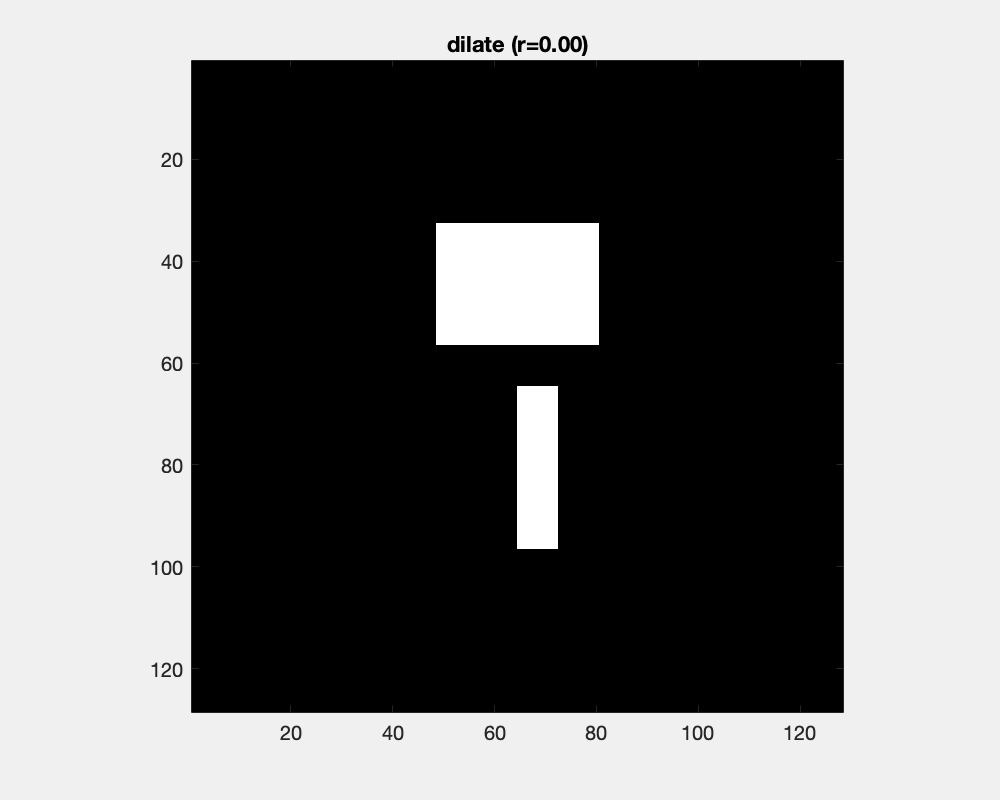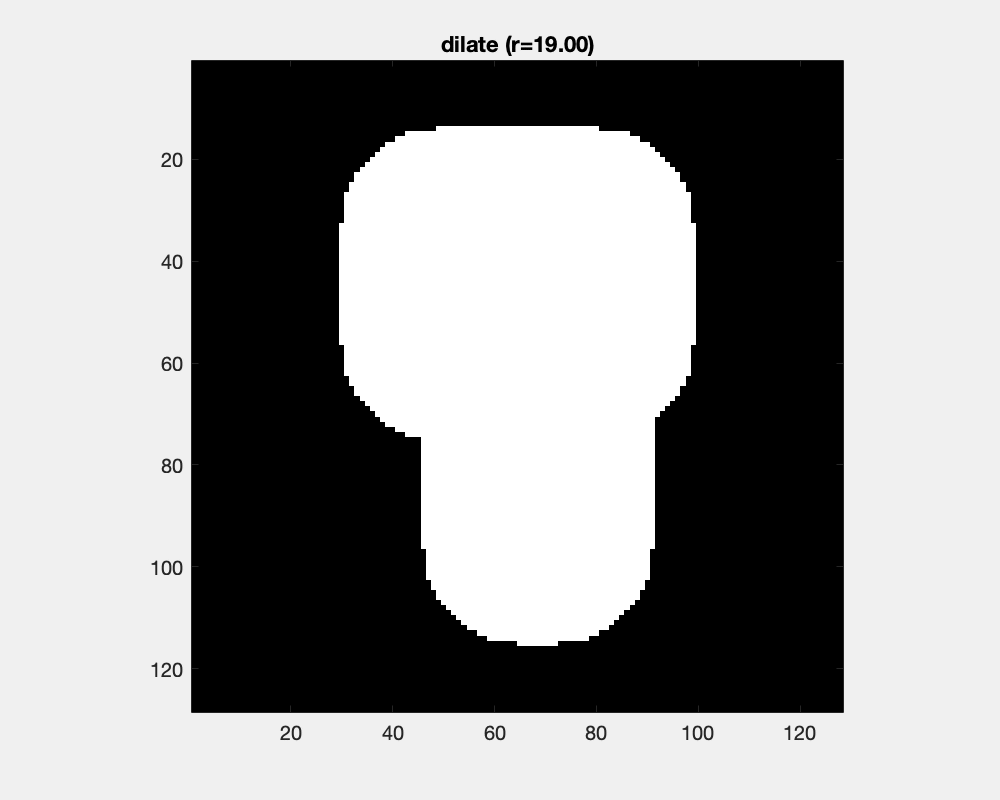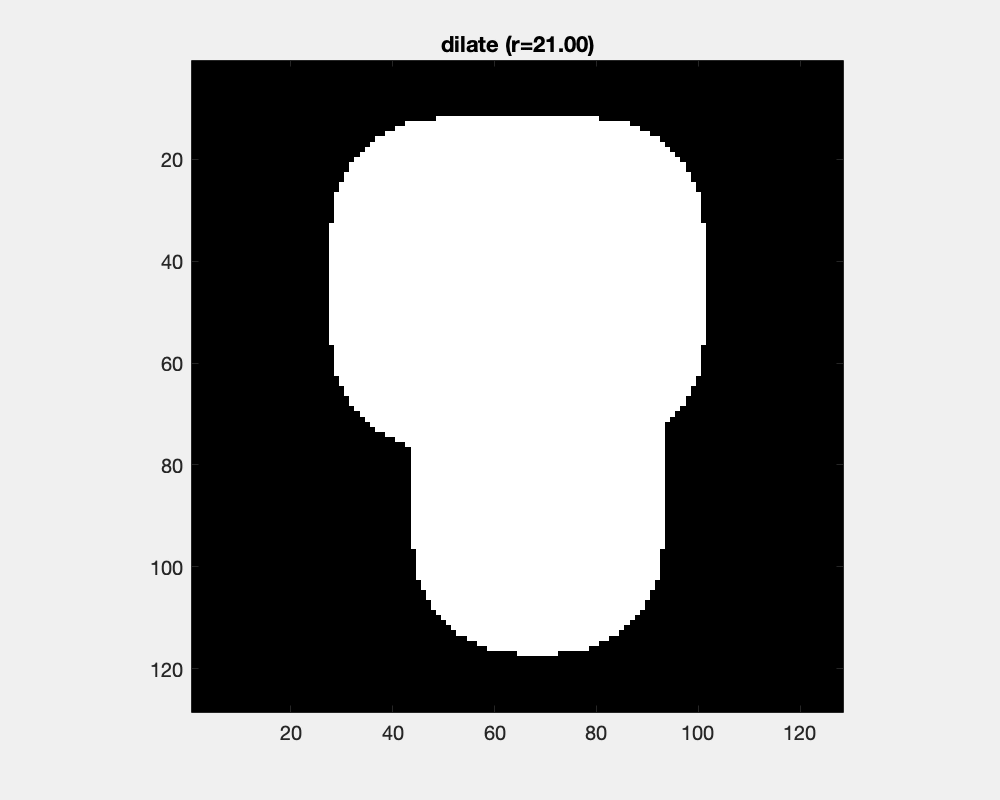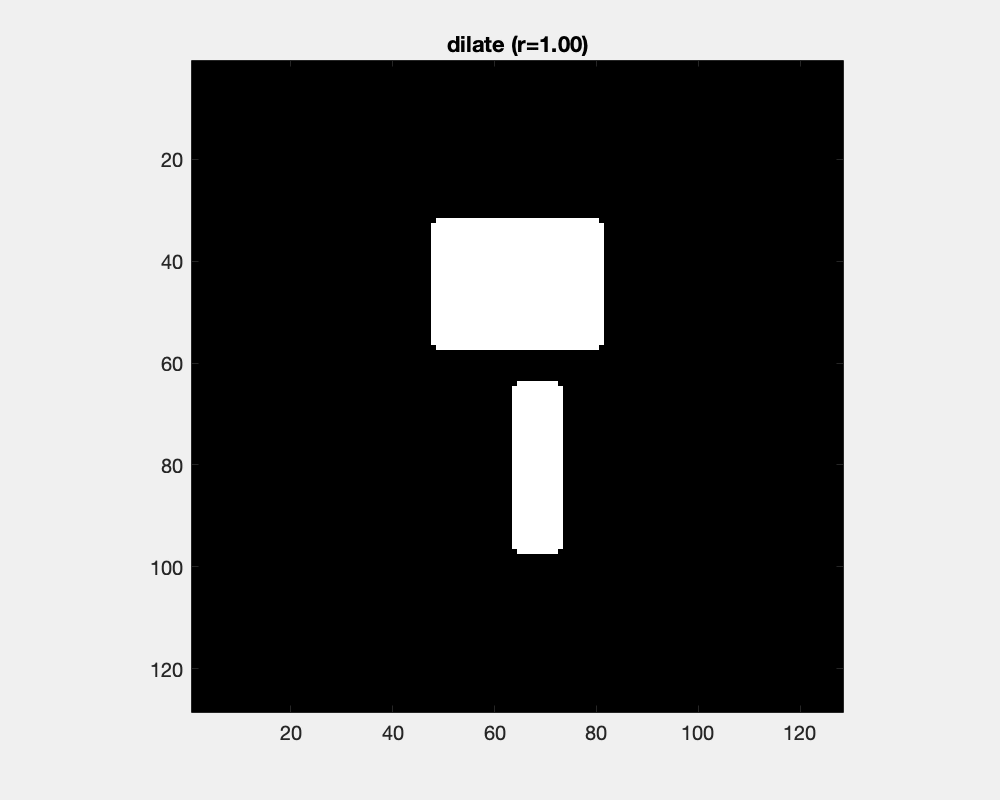
The size of the disc as a structure element influences the result of dilation: concave areas are filled and objects are joined.
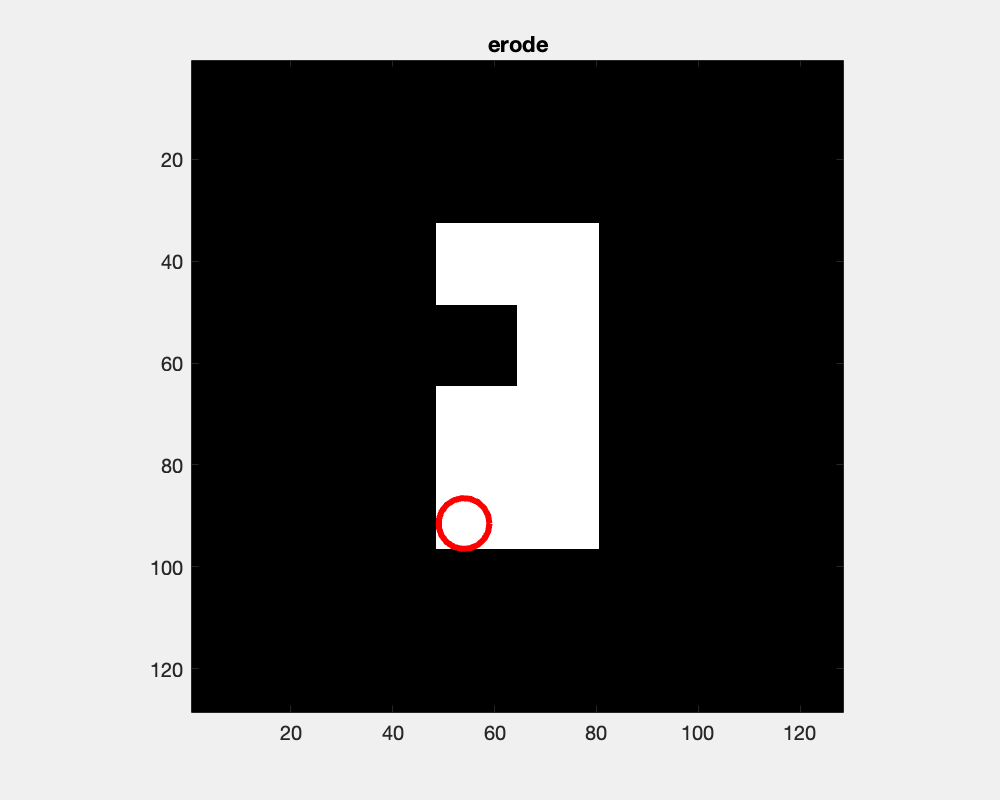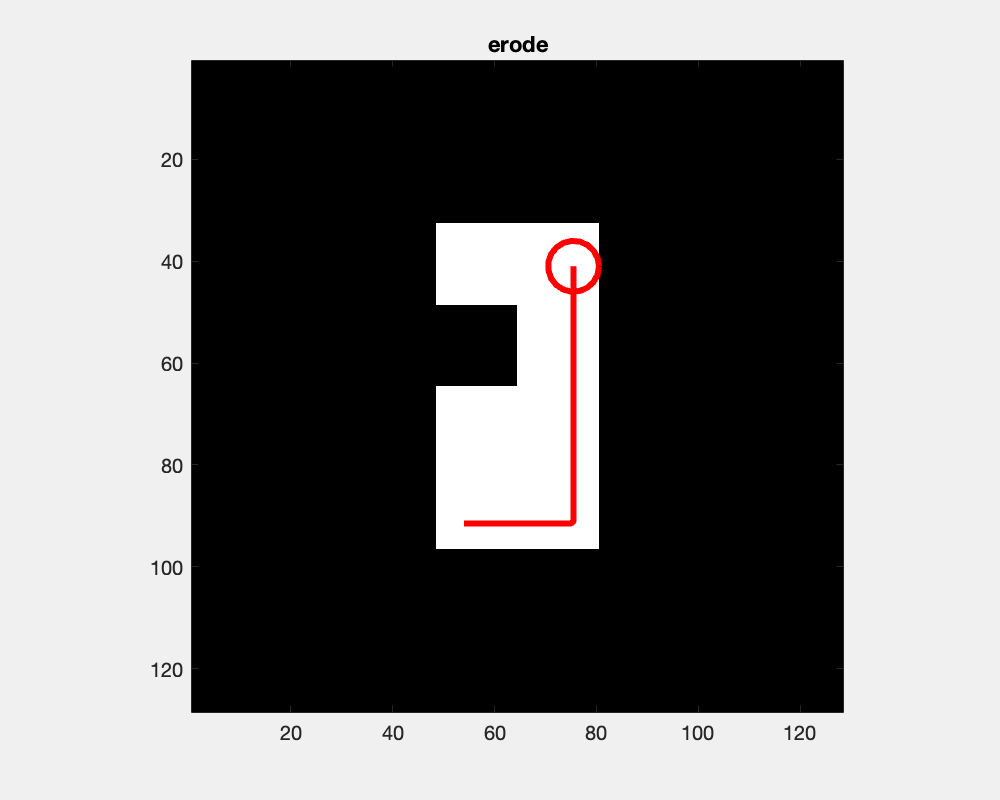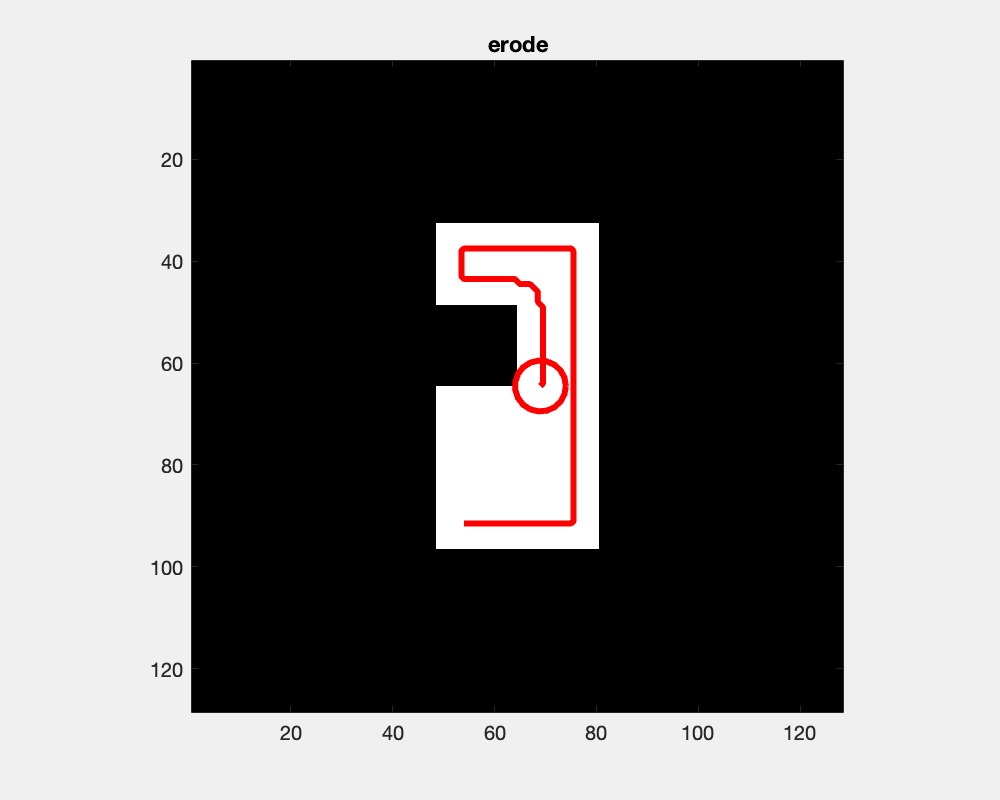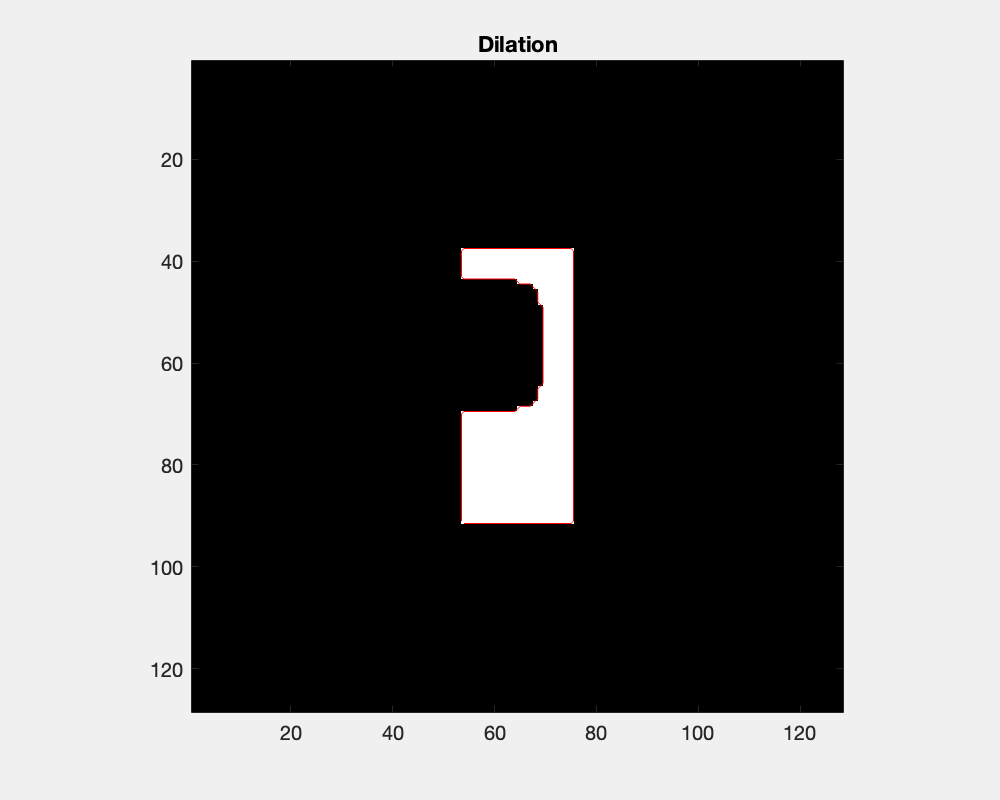
The effect of erosion with a disc-shaped structuring element can be envisioned as the locus of anchor points, here the center of the disc, as the element skims the surface on the inside of an object.
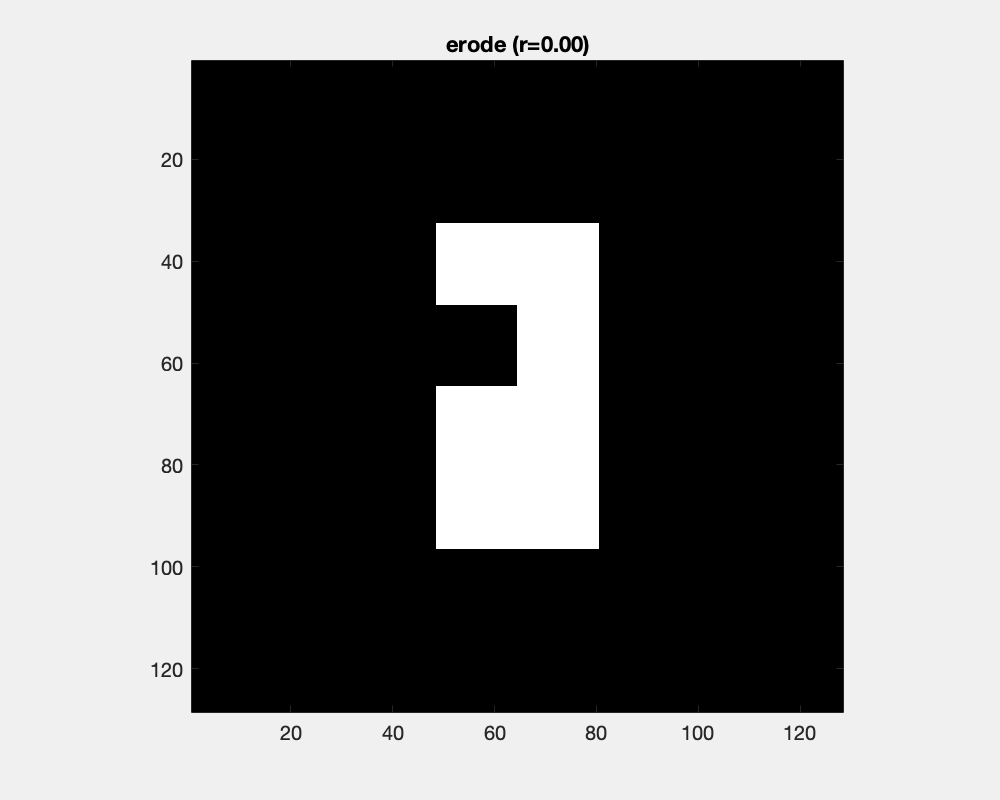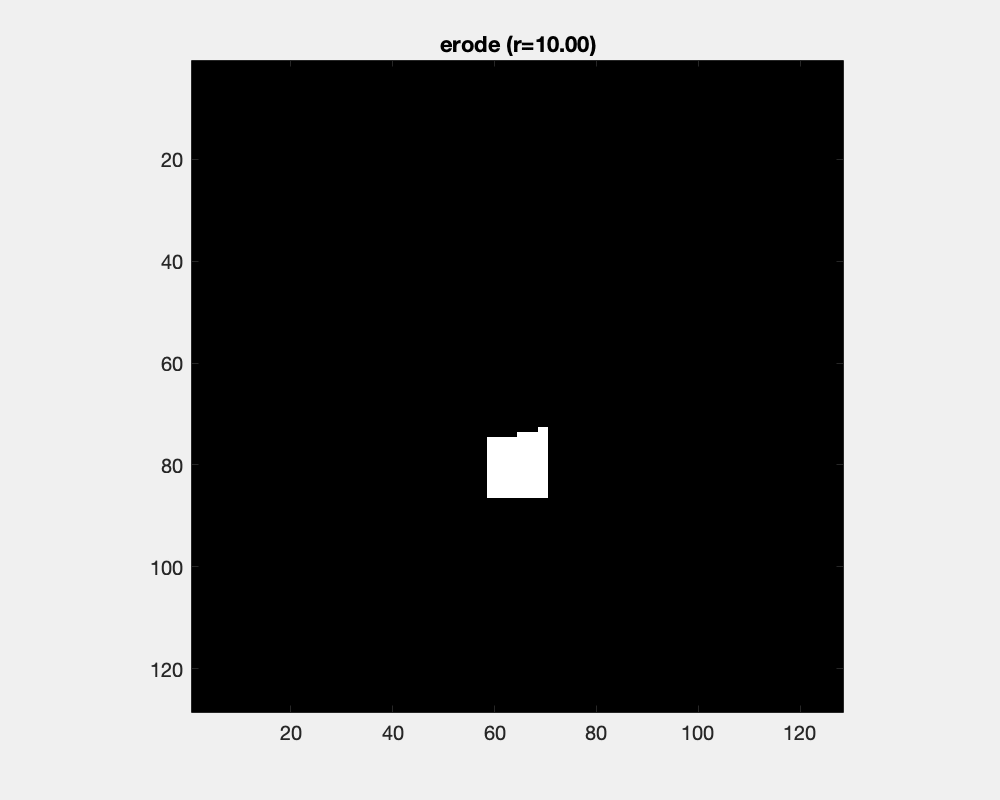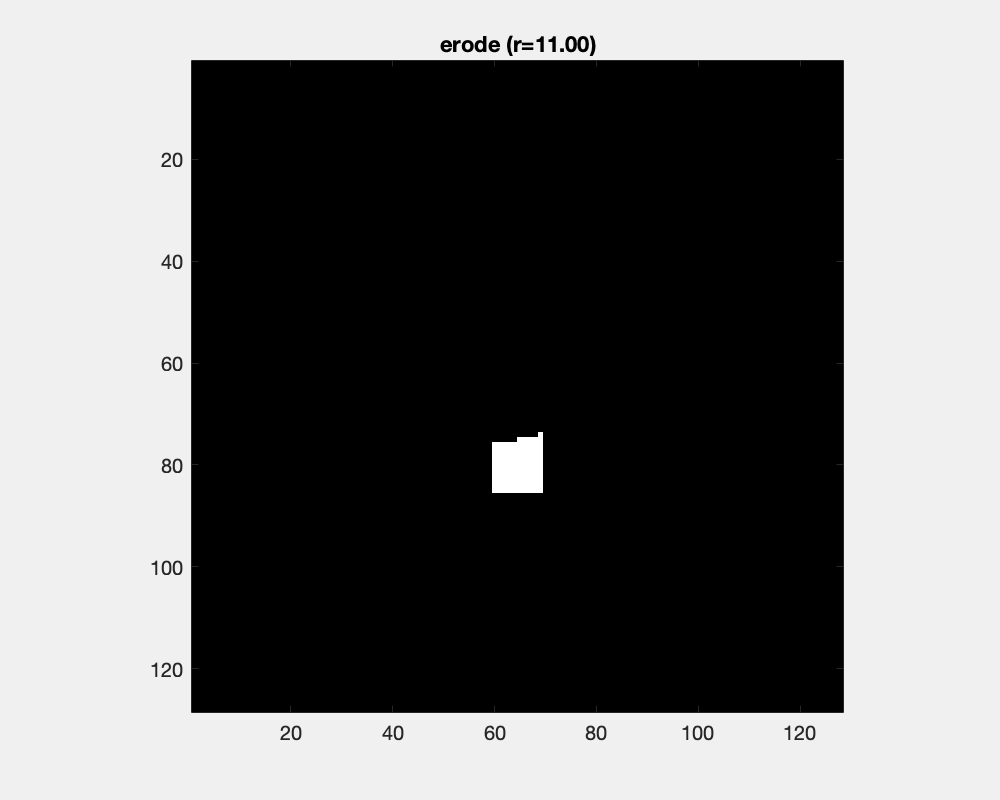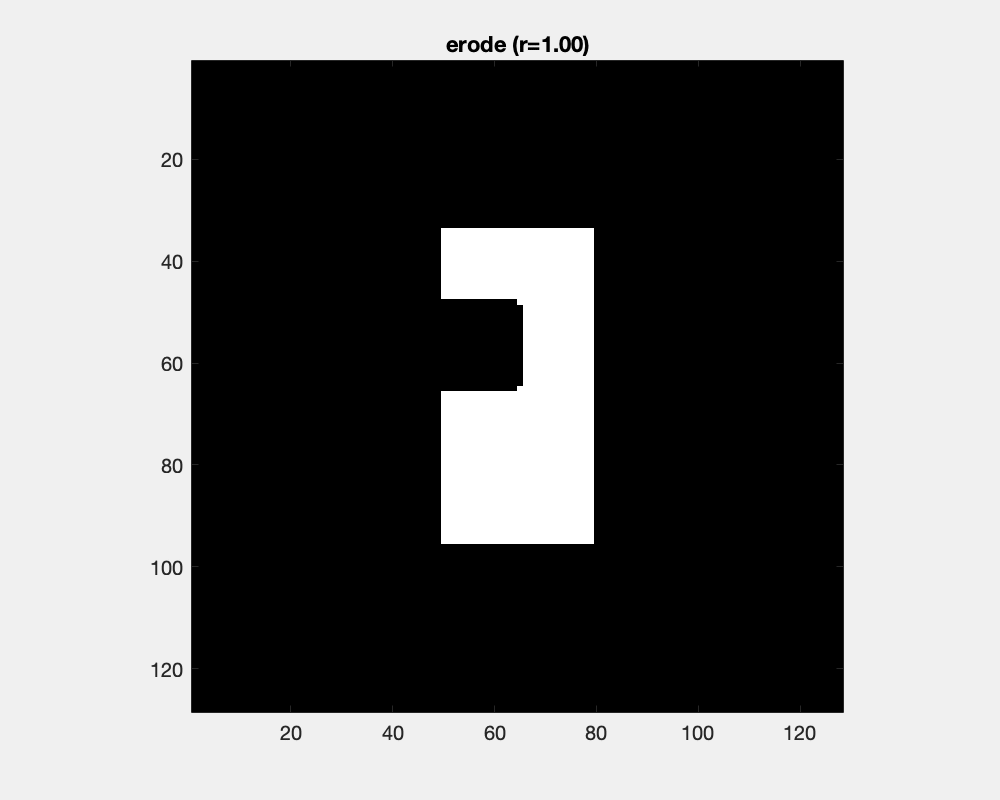
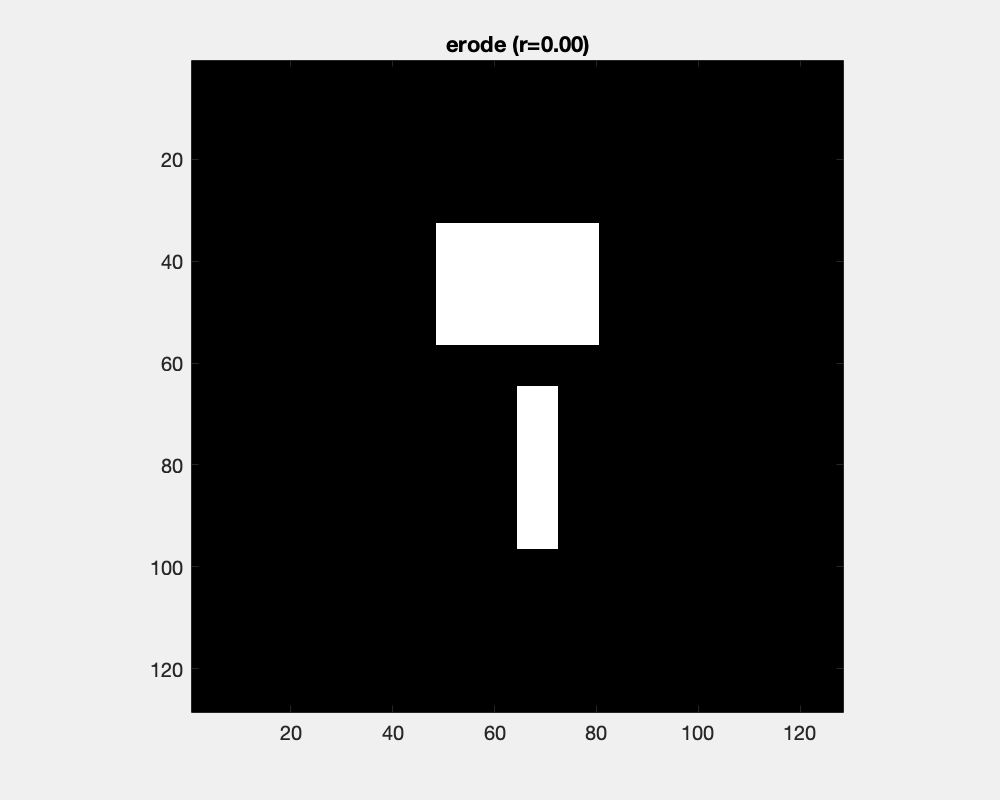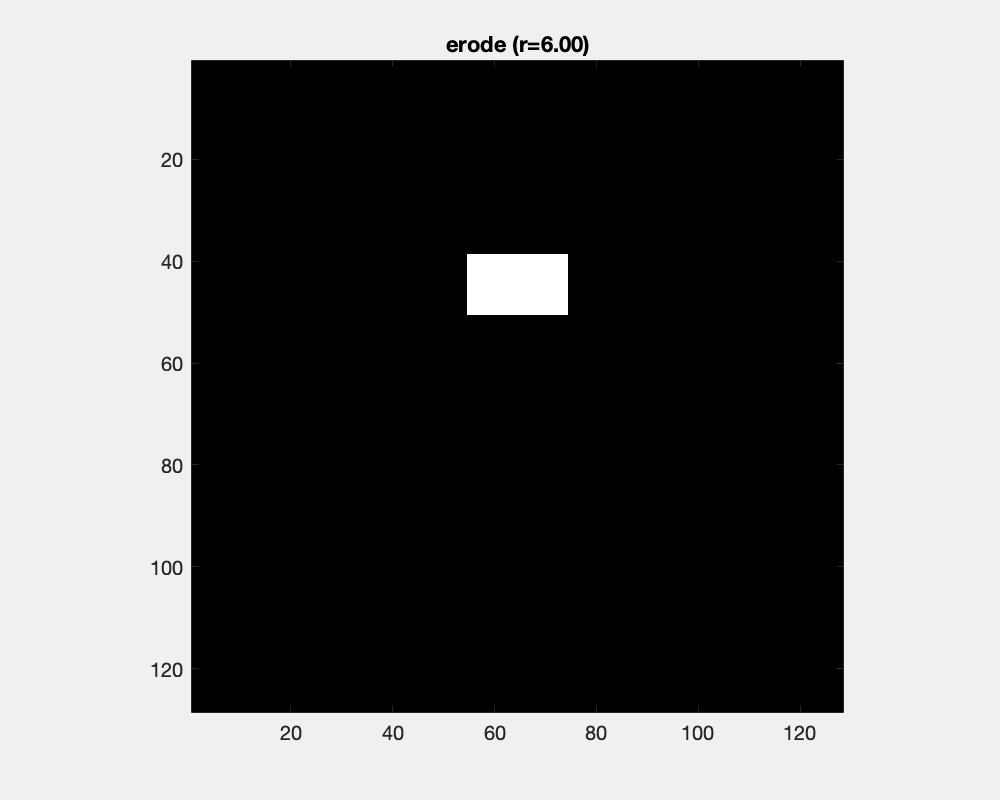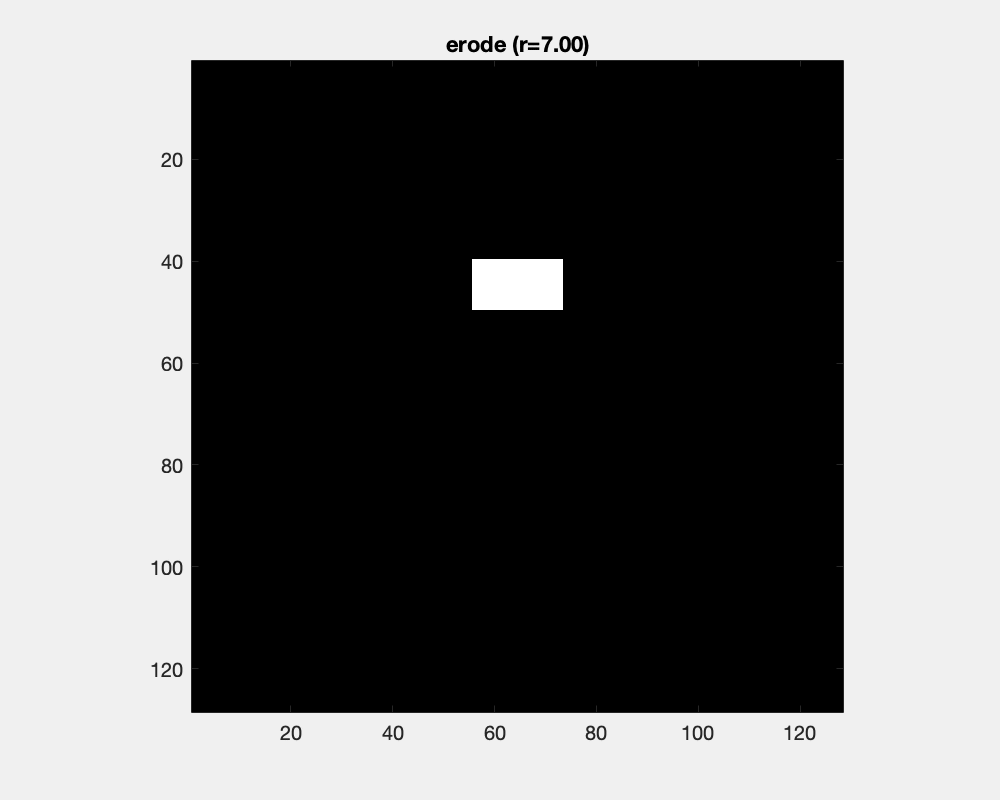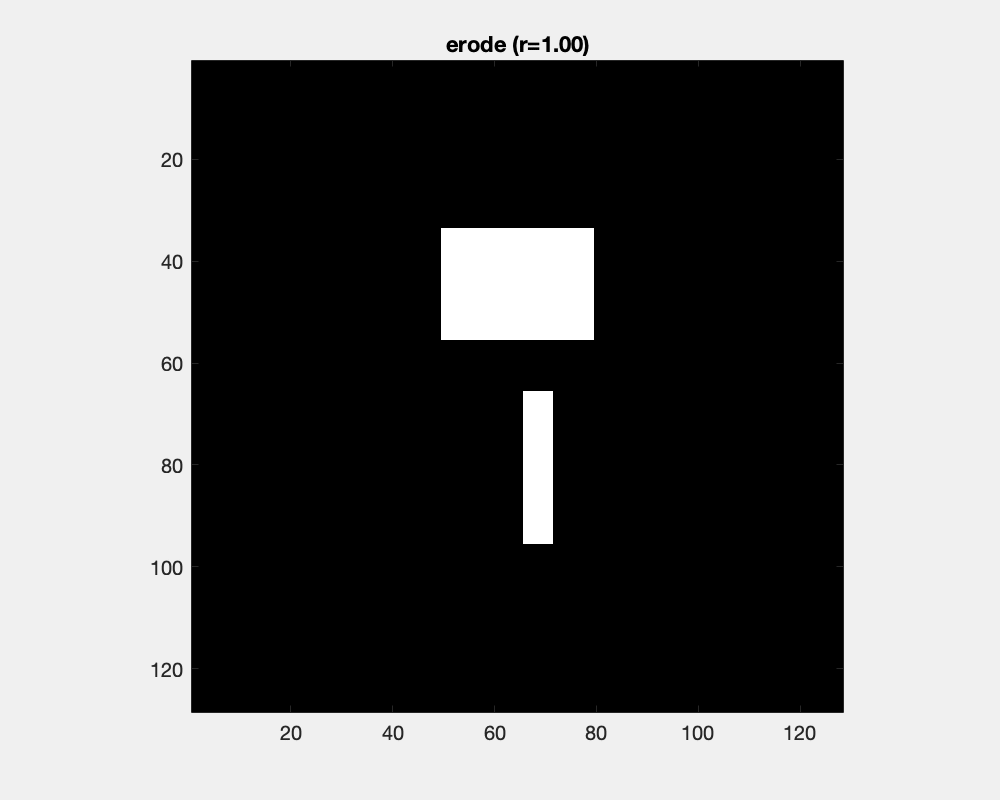
The size of the disc as a structure element influences the result of erosion: convex areas are cut off and small objects are deleted.
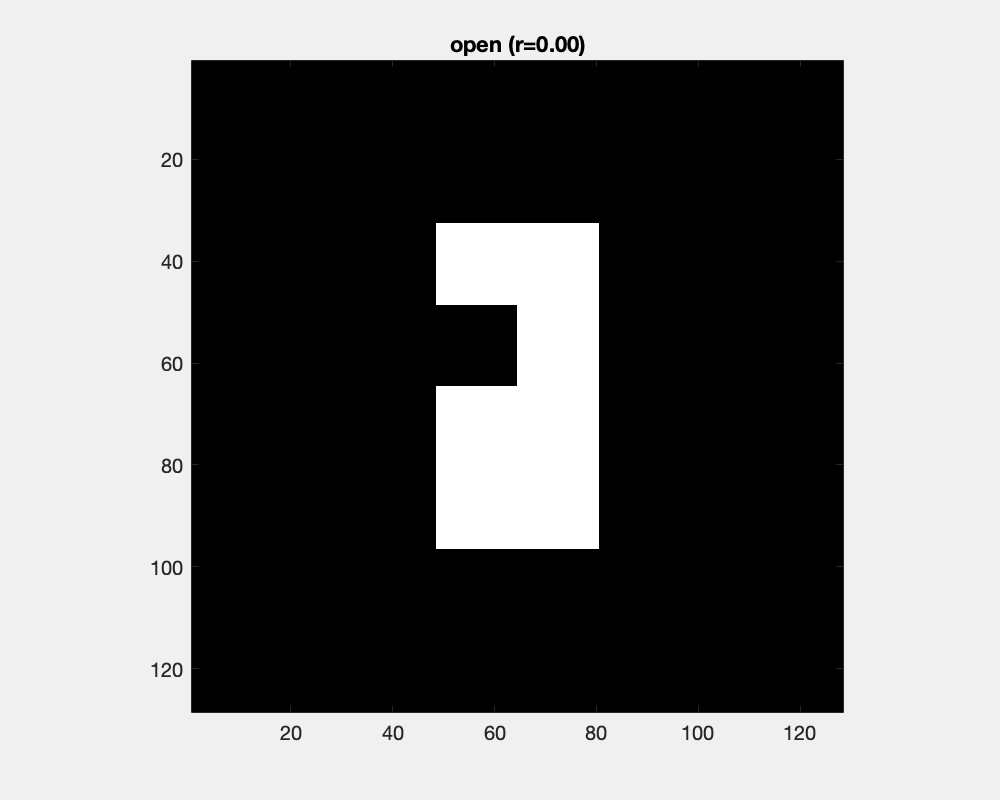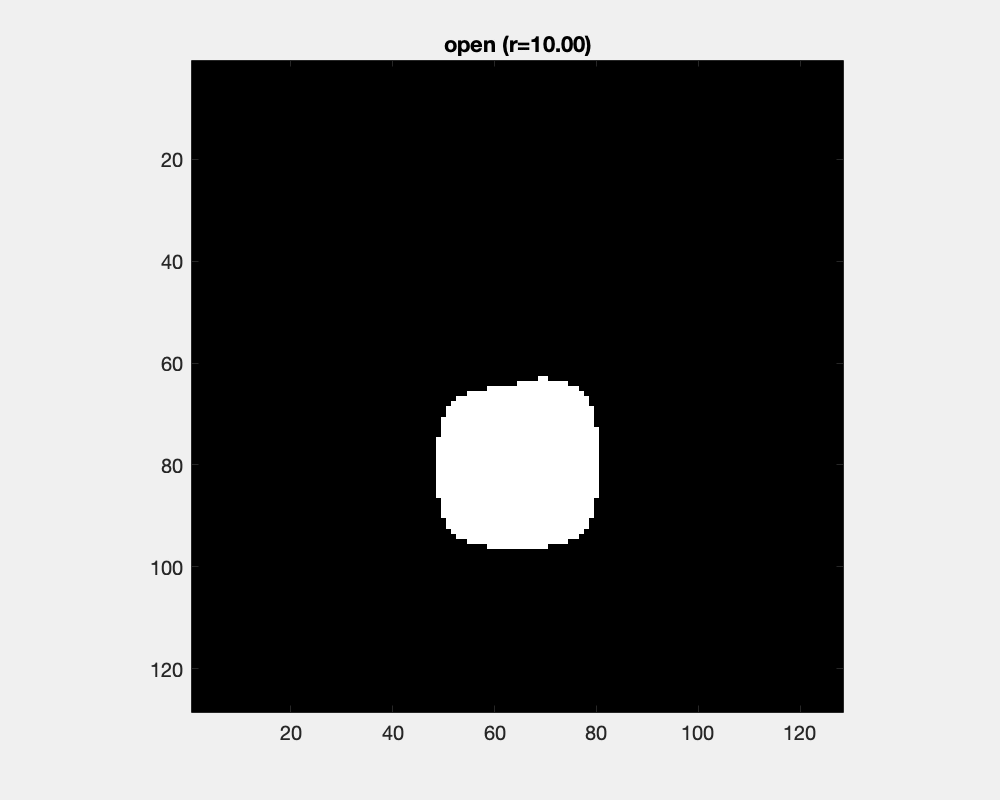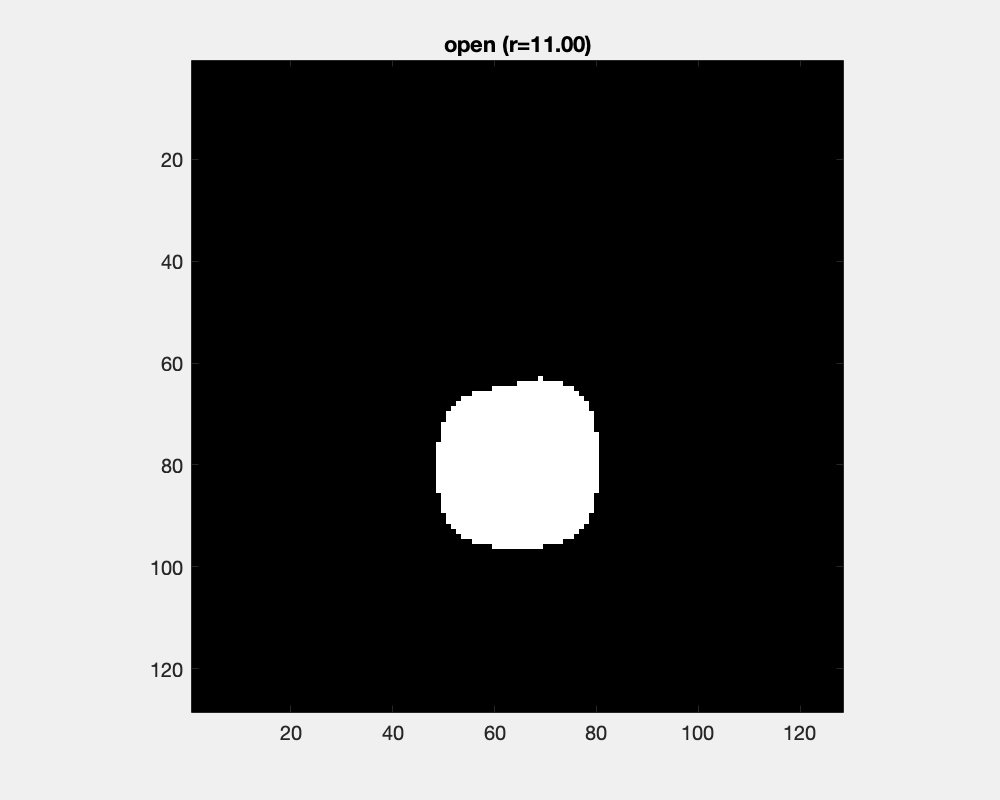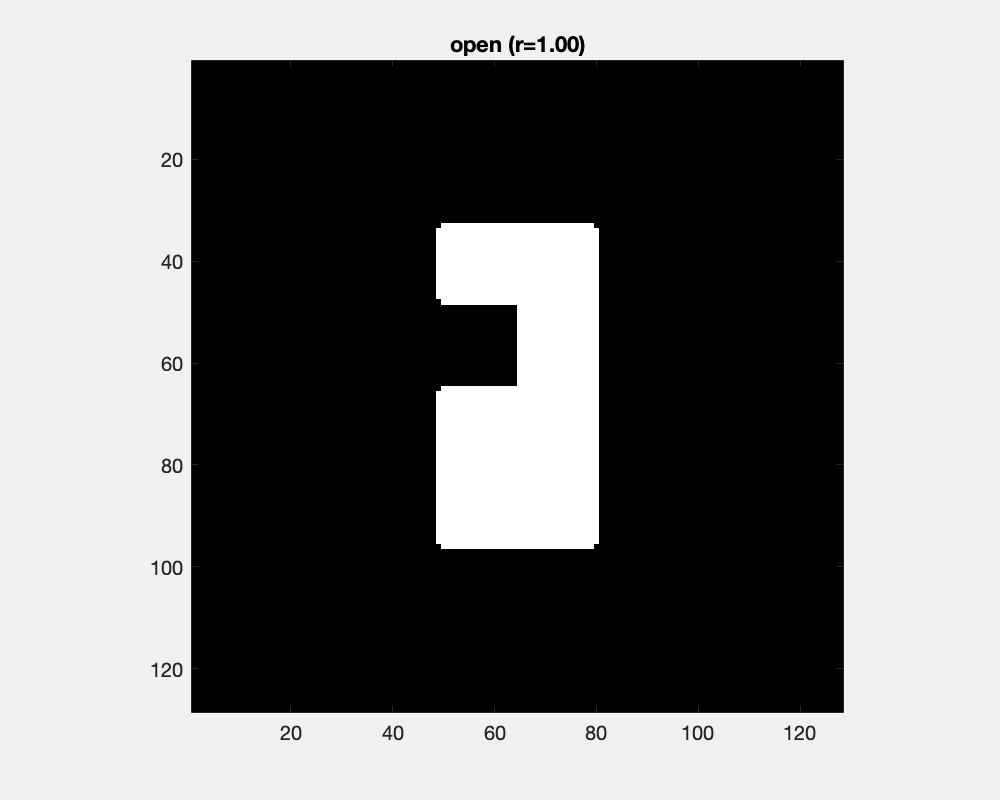
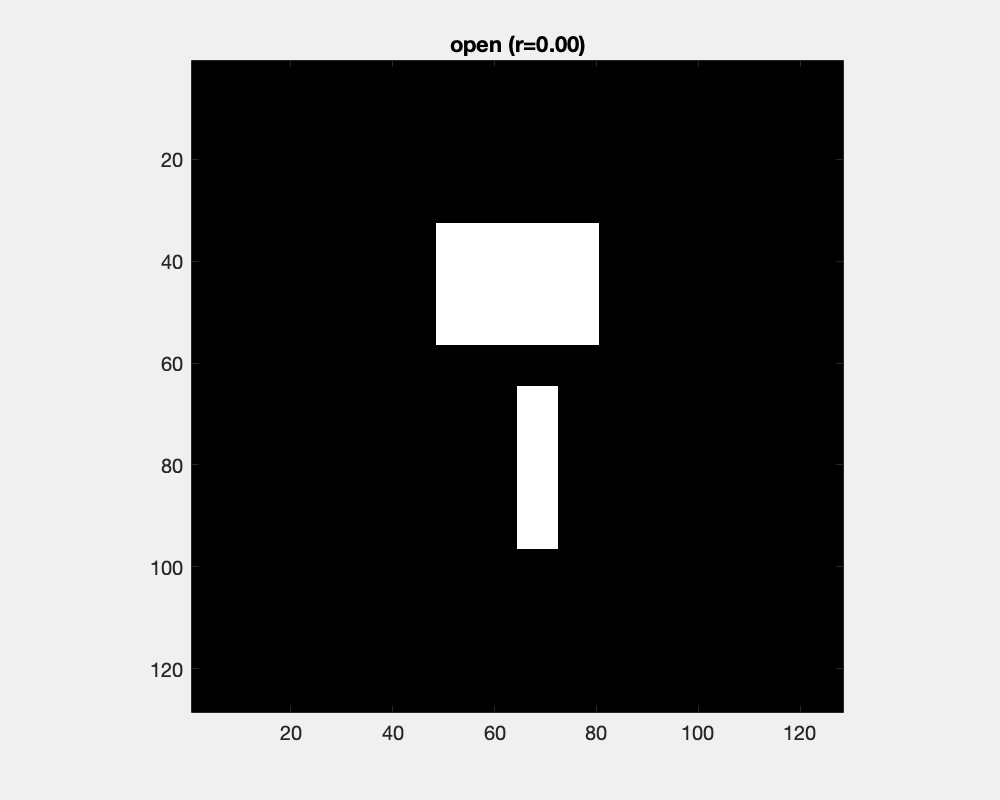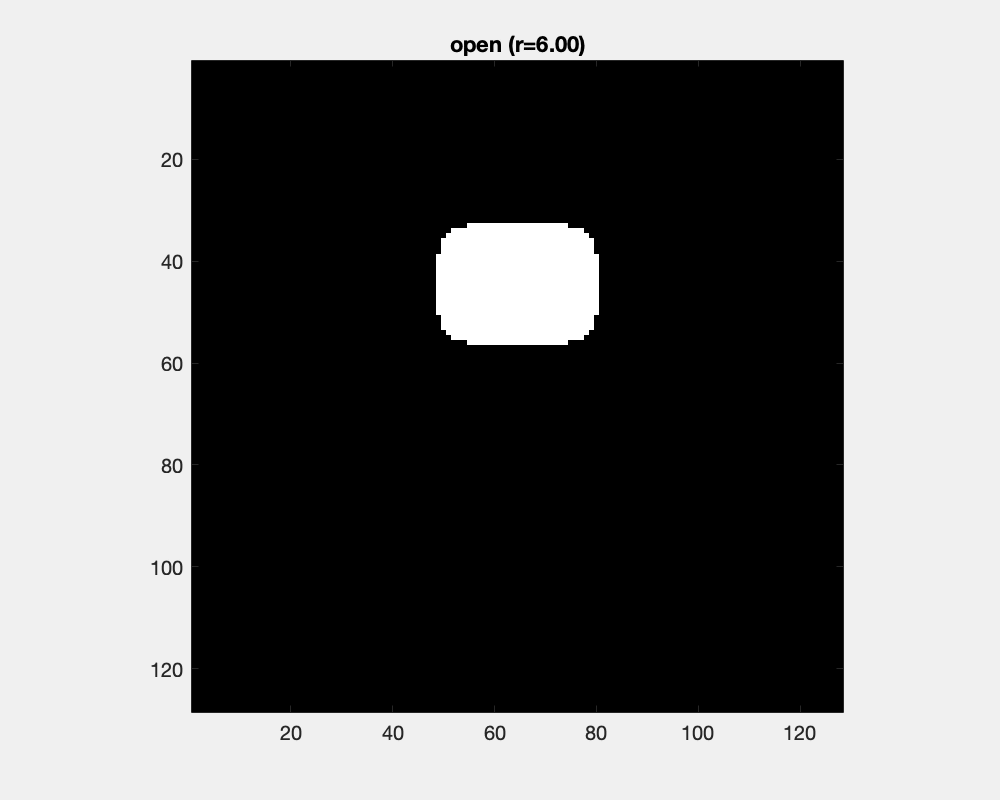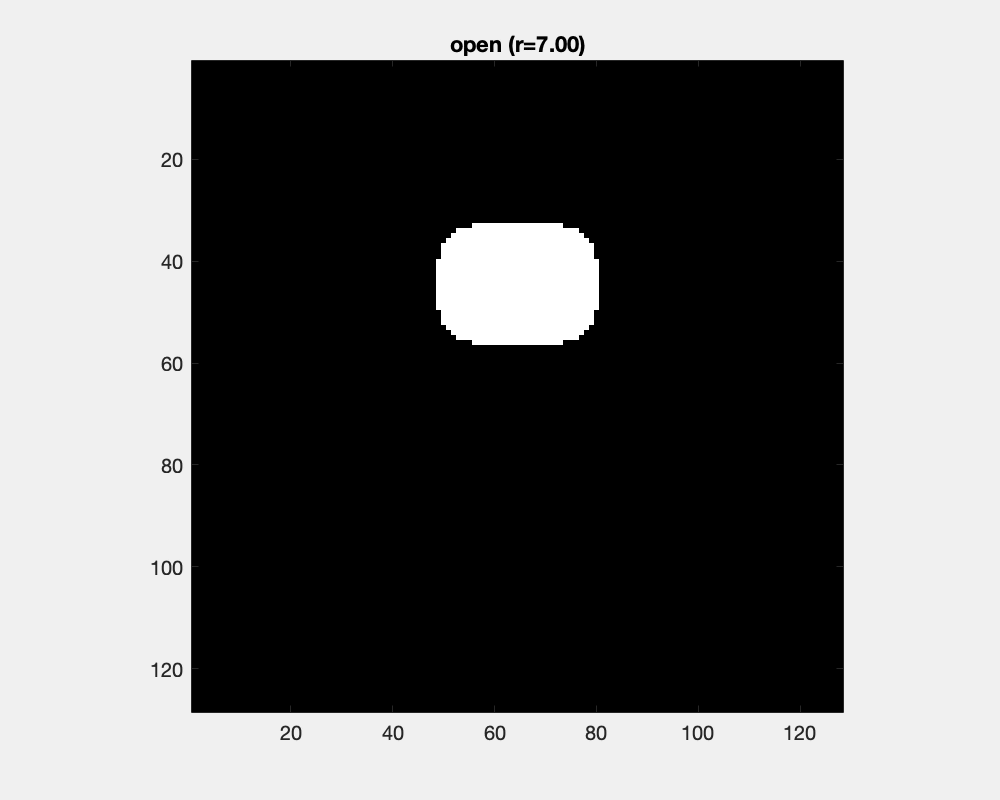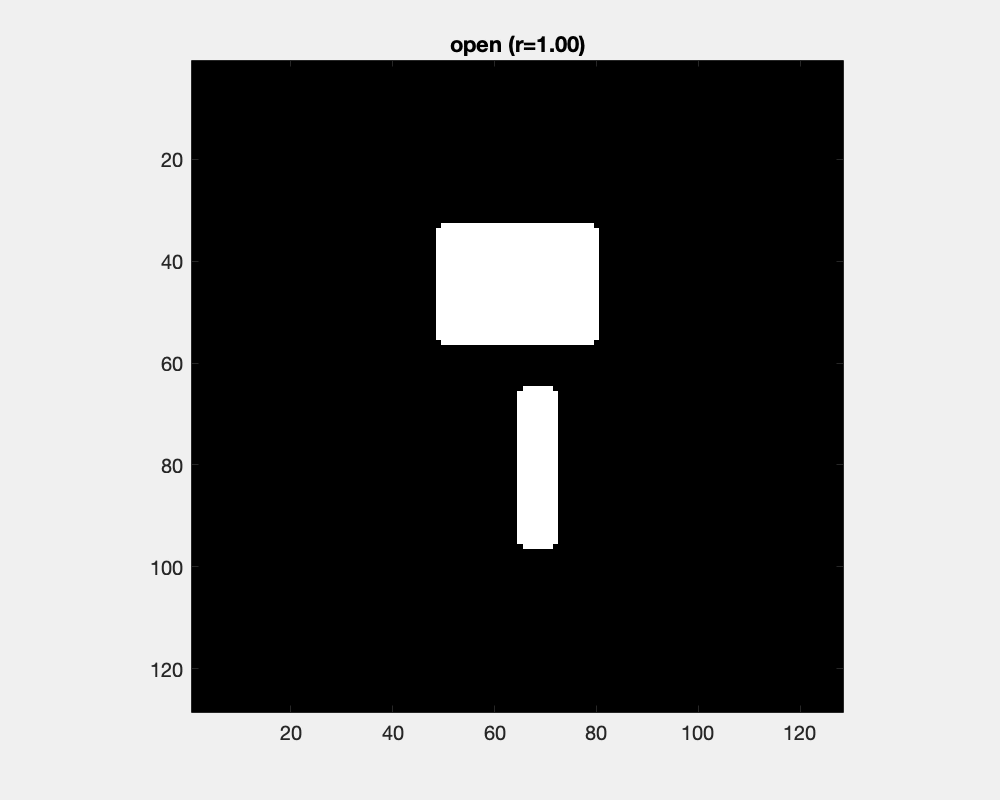
Erosion and dilation changes object's sizes dramatically. Counteracting an erosion with an ensuing dilation is the open operation. It has little effect for large objects and small structuring elements, while as the structure element grows, protrusions are separated into parts and eventually cut off and small objects are removed.
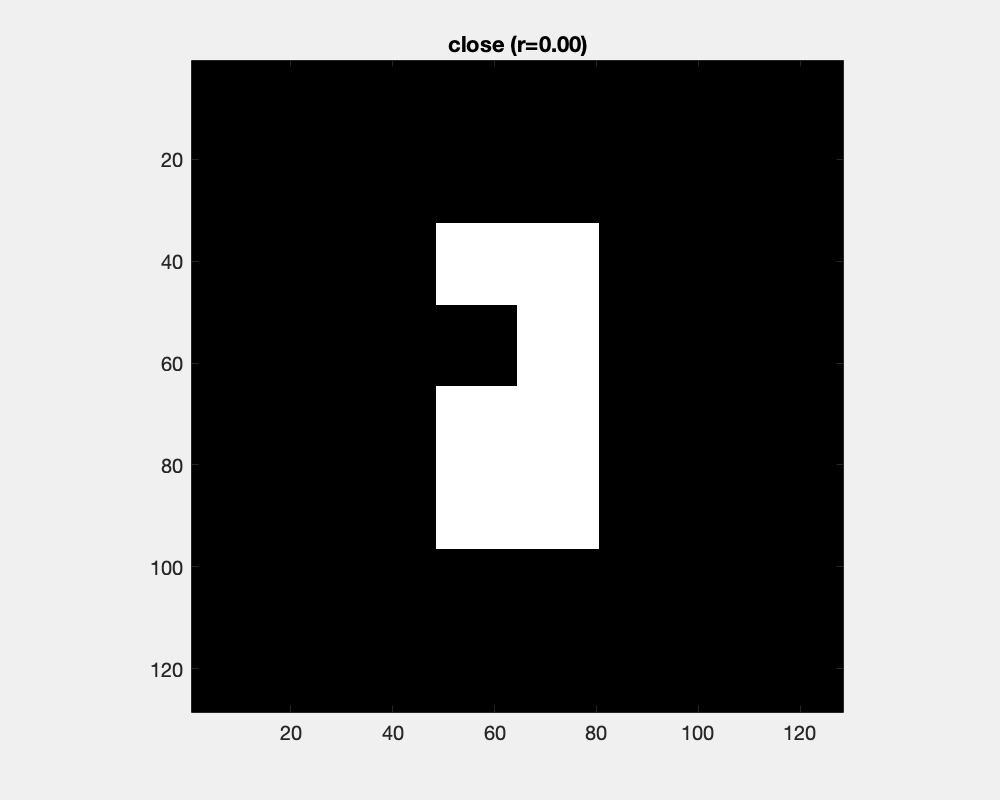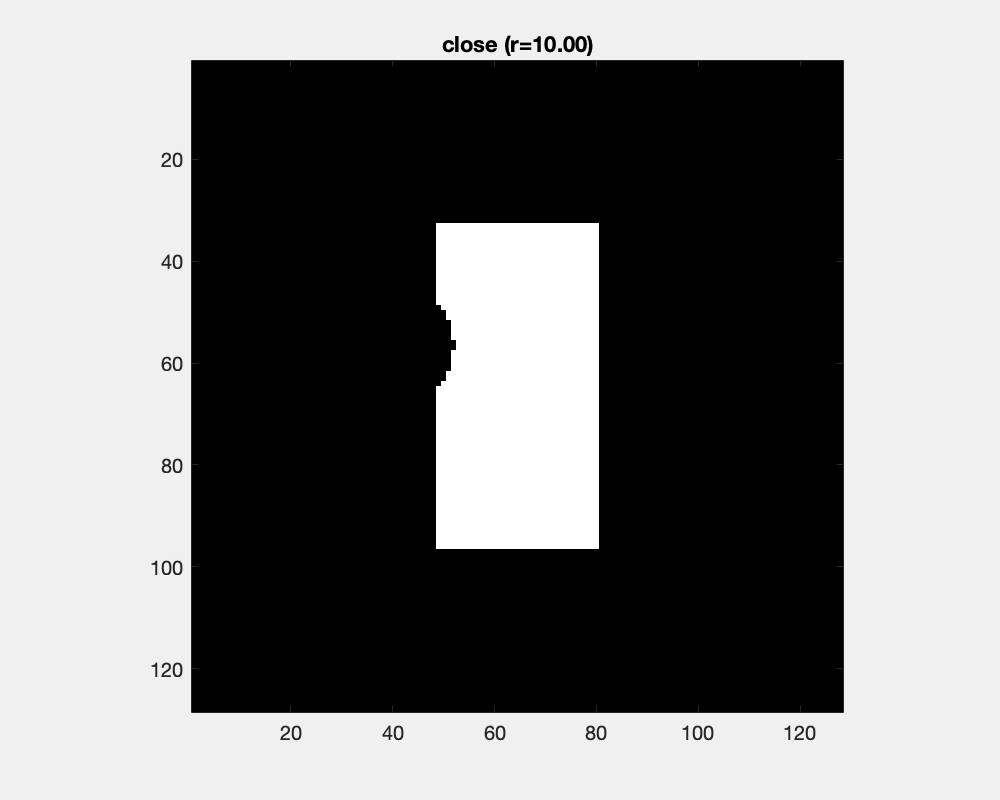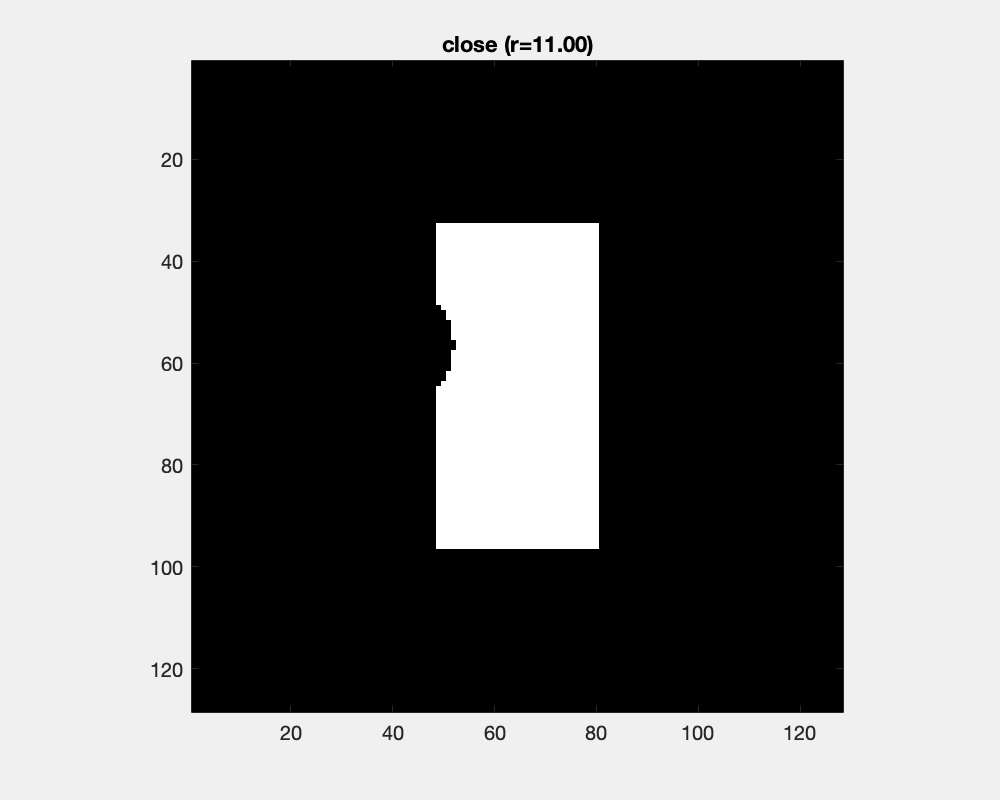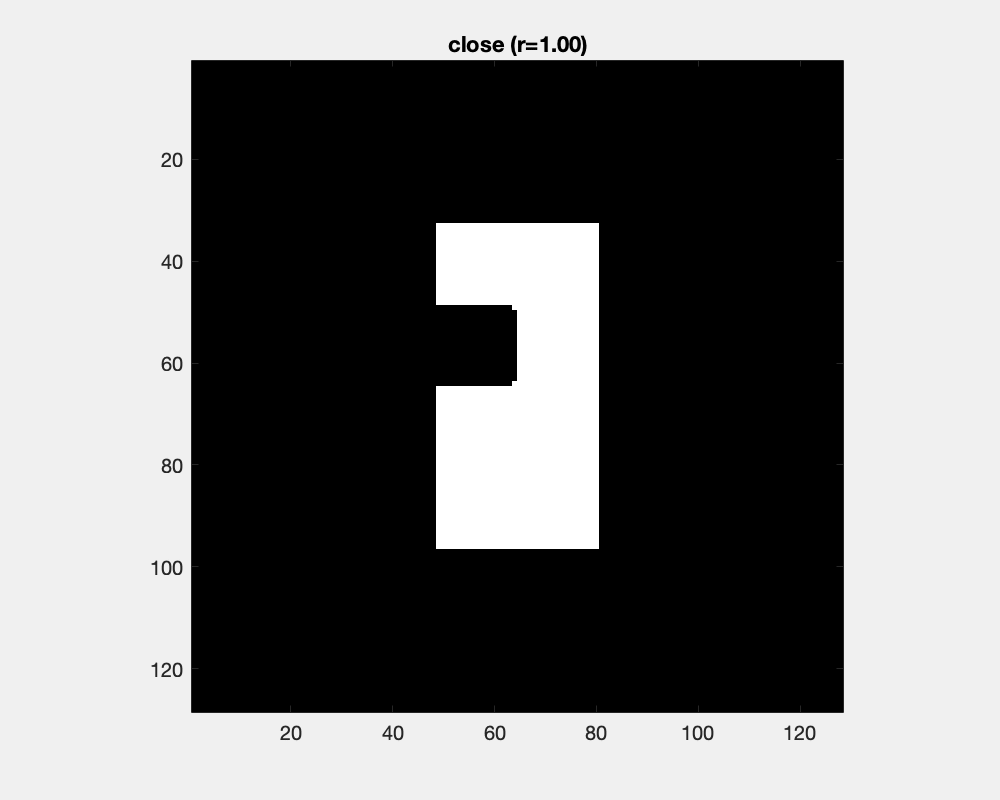
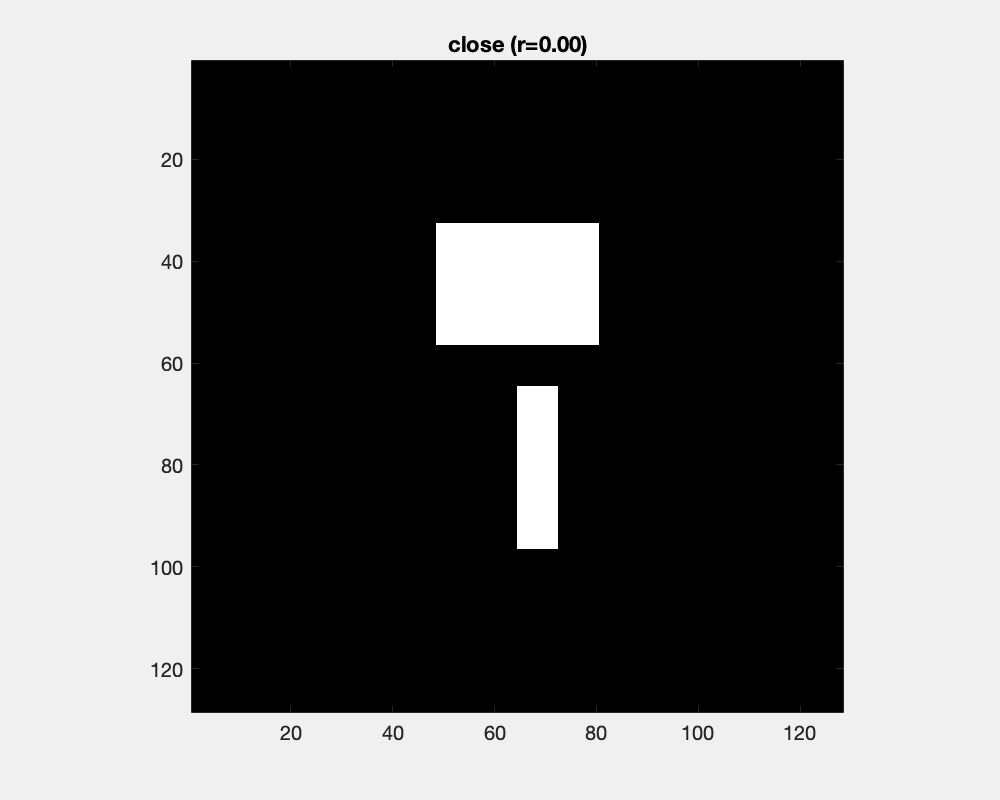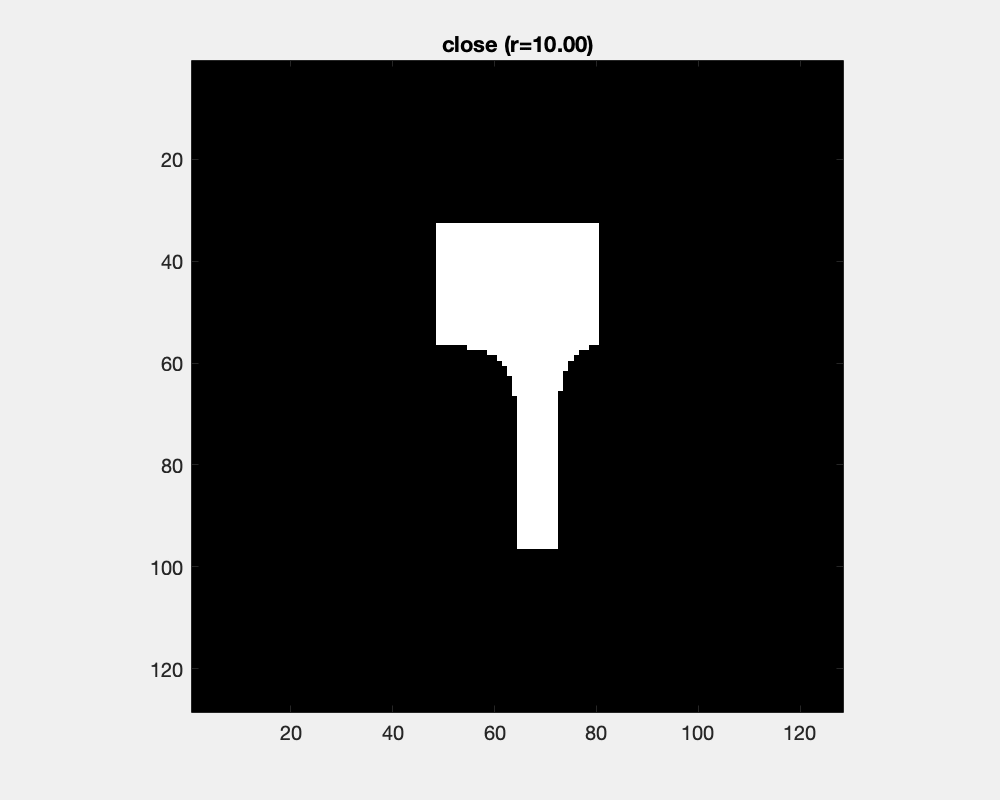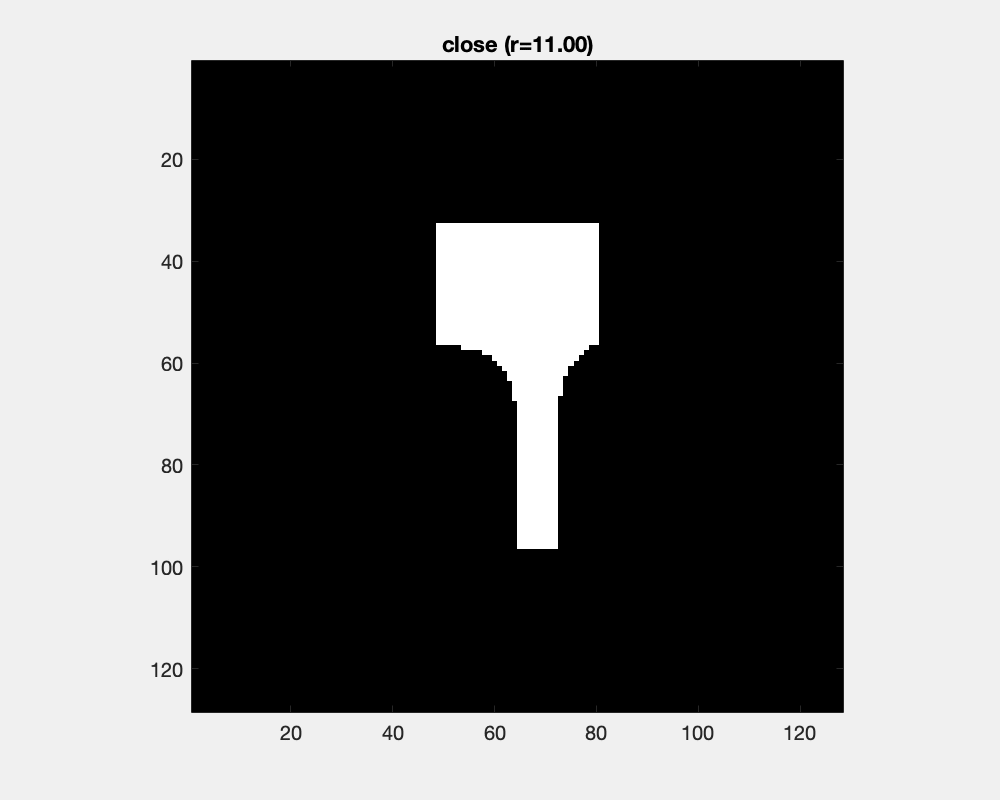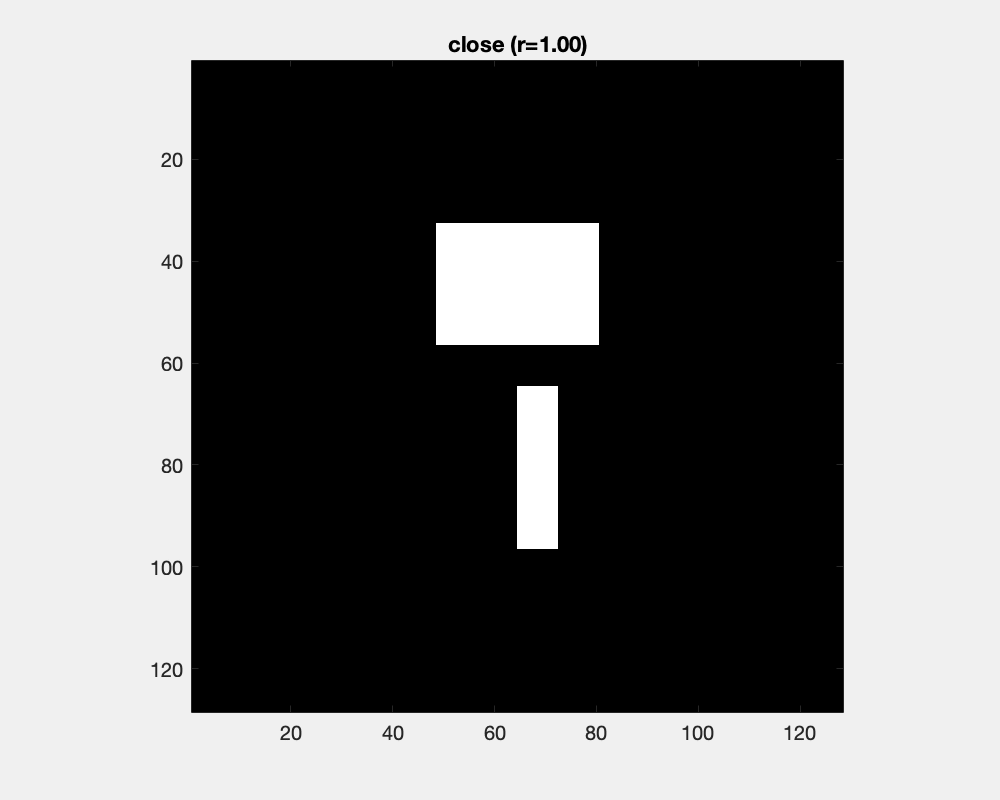
Dilation and erosion changes object's sizes dramatically. Counteracting an dilation with an ensuing erosion is the close operation. It has little effect for large objects and small structuring elements, while as the structure element grows, concave areas are filled and objects are joined.
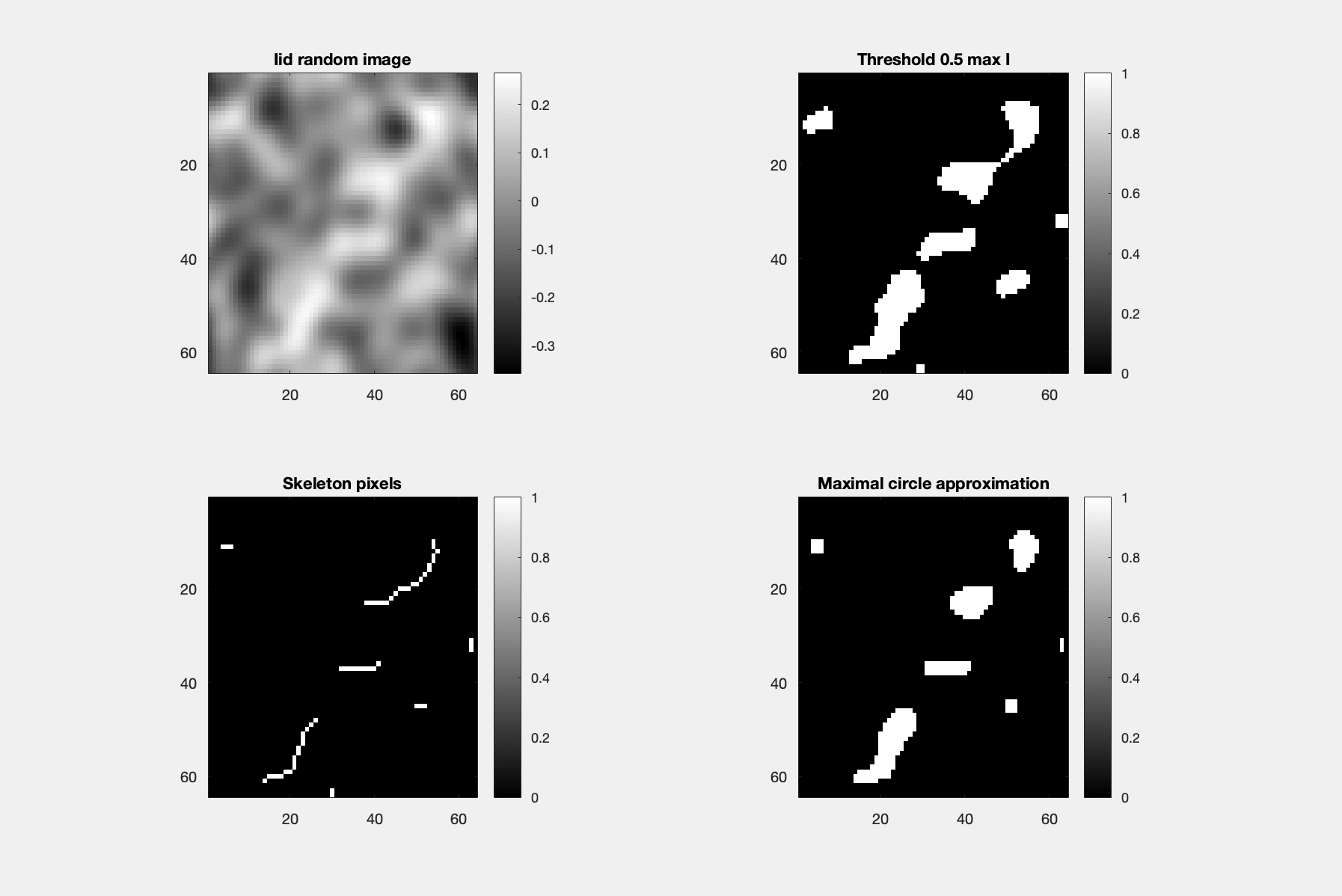
Identically and indepdendent distributed data (iid) smoothed and thresholded gives random shapes. The skeleton algorithm finds the locus of points of maximum circles that touch the object's boundary at least 2 places to at least 1st order (same location and same tangent). Bottom right image shows the reconstruction of the objects via the quench function, that is, the union of maximum circles centered on the skeleton.

A simple algorithm for calculating the quench function is to test circles centered an every skeleton point and seek the largest, for which the intersection is equal to the circle.
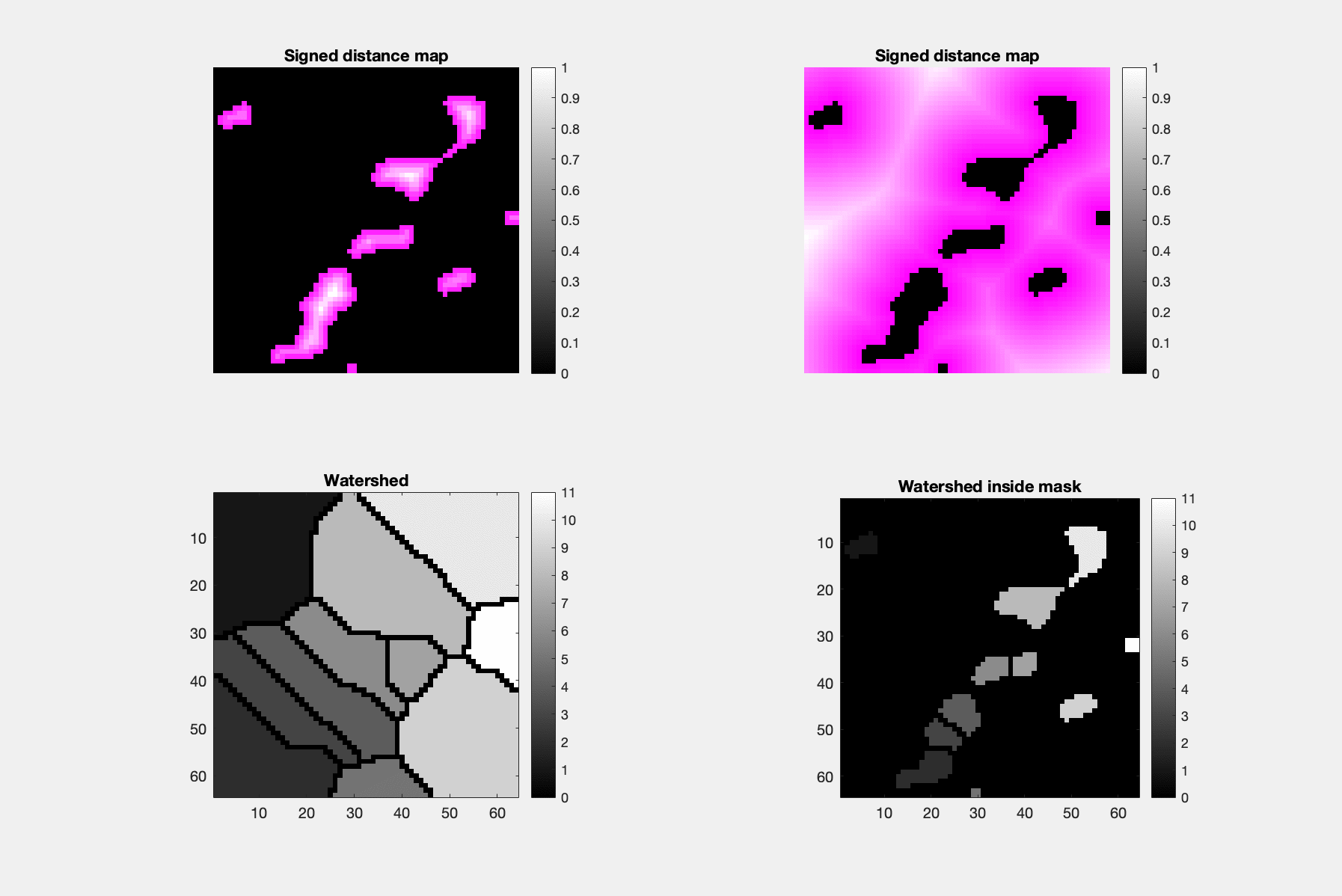
The signed distance, here showed without sign and seperately for the inside and the outside, may be calculated by erosion and dilation, and it's ridges are the skeleton points. Followed further by the watershed algorithm identifies parts of objects, which are signified by local thinning of objects.